Halo-in-Uranus
Earth Moon and Artificial Intelligence
Earth Moon and Artificial Intelligence
Abstract: Thermoelectric Effects Peltier Seebeck and Thomson
Full page: Thermoelectric Effects Peltier Seebeck and Thomson
Scattering of Directional Light
Blue Marble the Uniform Earth Image
The Sun and the Moon a Riddle in the Sky
Particles in a box
Boltzmann Transport Equation
Uri Lachish, Rehovoth
![]()
Abstract: A powerful tool to study transport phenomena. Currents and transport coefficients are calculated. Thermal diffusion, irreversible thermodynamics and thermoelectric effects are discussed.
Contents
1. Introduction
2. Boltzmann transport equation: Derivation of the equation.
3. The currents: particle, energy and heat currents.
4. The transport coefficients: Diffusion, electrical and thermal conductivity, Weidmann-Franz and Einstein relations.
5. Particles flow within a medium with a temperature gradient: Knudsen law
6. Irreversible thermodynamics
7. Charge Transport through a junction
New
8. Thermoelectric effects: Thomson, Peltier and Seebeck
New
9. Summary and conclusions
1. Introduction
Boltzmann Transport Equation is a powerful tool
for analyzing transport phenomena within systems that involve density and
temperature gradients. The equation is applied to analysis of the general
currents within a system, the transport coefficients and the relationships
between them. Thermally induced diffusion is discussed.
2. Boltzmann transport equation
Consider a system with
non-uniform particle density and temperature. In each place within the system
there is a local range where the thermal velocities are given by an equilibrium
distribution function. The distribution is temperature dependent and varies from
place to place.
A non-equilibrium distribution function determines the probability of a particle within the system to be at some place and to have some local thermal velocity. Boltzmann transport equation expresses the global non-equilibrium distribution in terms of local equilibrium distributions. The equation enables application of properties of equilibrium systems to the study of a non-equilibrium system.
Consider a system of randomly moving particles within a medium with a temperature gradient along the x-axis. Whenever a particle is scattered, or collides with the medium, its thermal velocity immediately after the collision will be that of the equilibrium distribution f0(x, T(x)) at the collision point.
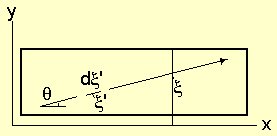
Figure 1: Particle moves within a medium in a ξ direction.
A particle moves with a
thermal velocity v in a ξ
direction at an angle θ with the x-axis (figure-1). The projection of
ξ on the axis is:
Δx = Δξ Cos(θ) (1)
The probability, dP, that the particle will collide with the medium along a distance element dξ is proportional to the length dξ , the density of the scattering centers ns, and their scattering cross sections σs :
dP = -P dξ Σ nsσs = -P dξ/l (2)
where the sum over s accounts for all different types of centers, and l = 1/(Σnsσs) is the mean free path.
The probability that the last collision of the particle, before reaching a cross section plane at some ξ , was along the element dξ', at a position ξ'. ( ξ' < ξ, figure (1)), is:
P(ξ') dξ'/l = e(ξ' - ξ)/ldξ'/l (3)
l
is determined by the properties of the medium and the name "mean free path" is justified, since-∞∫ξ(ξ' - ξ) P(ξ') dξ'/l = l, that is, l is the probable distance where the particle comes from.
The velocity distribution v of a particle, at the cross section plane ξ, is obtained by adding the local velocity distributions at all the distance elements along the line up to ξ. Each distribution is multiplied by the probability that the particle comes from that distance, namely, that it has collided for the last time with the medium at that place :
f(ξ,v) = -∞∫ξf0(ξ',v) P(ξ') dξ'/l (4)
where v = |v| and f0( ξ', v) is the local equilibrium distribution at ξ'. If the equilibrium distribution does not change significantly along the mean free path l, it will be possible to use the first terms of Taylor series:
f0(ξ',v) = f0(ξ,v) + (∂f0/∂ξ) (ξ' - ξ) + (∂f0/∂v) (v(ξ') - v(ξ)) (5)
The change in velocity is a result of force acting on the particle. For example, a gravitational field, or an electric field for a charged particle. Assuming that the force acts in the x-direction, the velocity change will be:
v(ξ')2 - v(ξ)2 ≈ 2v (v' - v) = 2a (ξ' - ξ) Cos(θ) (6)
where a is the acceleration, equal to eE/m for an electric field E.
Substituting (6) and (5) into (4), integrating over ξ', and finally substituting x and θ for ξ according to (1):
f(x, v, θ) = f0(x, v) - l Cos(θ) [( ∂f0 / ∂x) + (a/v) (∂f0/∂v)] (7)
The non-equilibrium distribution (7) is the linear Boltzmann transport
equation in a somewhat non-traditional form.
f0(x, v) is the local equilibrium distribution given by Maxwell-Boltzmann or
Fermi-Dirac distributions. The medium properties enter through the mean free
path l, and external forces
through the acceleration a. The standard form of the linear
Boltzmann transport equation includes a constant relaxation time τ,
∂f/∂t + v gradx(f) + a gradv(f) = -(f - f0)/τ
, where τ =
l/v .
3. The currents
A particle moving at a velocity v will cross a plane section at x during a
time Δt if its distance from
the plane is less than
|v| Cos(θ)
Δt.
The particle current through a unit cross section at x is obtained by summing all the velocities of all directions in space (spatial angle of 4π), each velocity weighed by the distribution probability:
Jn = ∫f(x, v, θ) |v| Cos(θ)d3v (8)
where d3v = 2π v2 dv Sin(θ) dθ. Substitution of the distribution function (7) into (8) yields the current:
Jn = -(4πl/3) [(eE/m) ∫(∂f0/∂v) v2 dv + ∫(∂f0/∂x) v3 dv] (9)
where the f0 contribution in (7) is zero, and
the trigonometric integral is
∫Cos2(θ) Sin(θ) dθ = 2/3.
Since the energy associated with each particle is (1/2)mv2 the energy current will be:
Ju = (m/2) ∫f(x, v, θ) |v|3 Cos(θ) d3v (10)
and by similar calculation:
Ju = -(4πl/3) [(eE/m) ∫(∂f0/∂v) v4 dv + ∫(∂f0/∂x) v5 dv] (11)
The currents will now be calculated by applying Maxwell-Boltzmann distribution:
f0(x, v) = n(x) (m/(2πkT))3/2e-m v^2/(2kT) (12)
where n(x) is the local particle density. The
pre-exponential factor in (12) is determined by the normalization condition:
0∫∞4π v2 f0 dv = n.
Since, (by (12)):
∂f0/∂v = -(mv/kT) f0 (13)
then:
Jn = (4πl/3) (eE/kT - d /dx) ∫f0 v3 dv (14)
Transforming to a dimensionless variable x = (m/2kT)1/2 v,
the integral will be:
∫f0 v3 dv = n (m/(2πkT))3/2 (2kT/m)2
∫x3 e-x^2 dx =
(nπ) (kT/2πm)1/2,
since
∫x3 e-x^2 dx = Γ(2)/2 = 1/2 (Appendix A).
The particle current is then:
Jn = [(4l/3)/(2πm)1/2] [eEn/(kT)1/2 - d(n(kT)1/2)/dx] (15)
A similar calculation yields the energy current:
Ju = (4πl/3) (m/2) (eE/kT - d /dx) ∫f0 v5 dv (16)
The integral is:
∫f0 v5 dv =
n (m/(2πkT))3/2 (2kT/m)3
∫x5 e-x^2 dx =
(nπ) (2kT/m) (kT/2πm)1/2,
since
∫x5 e-x^2 dx = Γ(3)/2 = 1 (Appendix A).
The energy current is then:
Ju = 2[(4l/3)/(2πm)1/2] [(kT)1/2 eEn - d(n(kT)3/2)/dx] (17)
or, by combining (15) and (17):
Ju = 2kT Jn - 2[(4l/3)/(2πm)1/2] n (kT)1/2 d(kT)/dx (18)
This equation expresses the energy current as a sum of two terms. The first is convection, the energy associated with the particle flow; and the second is heat conduction, which is proportional to the temperature gradient and independent of the particle current.
In electrical conductors (but not in semiconductors) the charge density does not depend on the temperature. The electrical current Jq will then be (by (15):
Jq = eJn = e [(4l/3)/(2πm)1/2] (1/kT)1/2 [eEn - (n/2) d(kT)/dx] (19)
4. The transport coefficients
The transport coefficients are
determined directly from the currents in equations (15)-(19). The diffusivity
D, defined by
Jn(dT/dx = 0, E = 0) = -D dn/dx, is:
D = [(4l/3)/(2πm)1/2] (kT)1/2 (20)
The electrical conductivity σ,
defined by Jq =
eJn(dn/dx = 0, dT/dx = 0) = σE, is:
σ = [(4l/3)/(2πm)1/2]e2 n/(kT)1/2 (21)
The thermal conductivity, defined by Ju(Jn = 0) = -K dT/dx, is:
K = 2[(4l/3)/(2πm)1/2] (kT)1/2 k n (22)
By comparing these coefficients, the Wiedemann-Franz law:
K/σ = 2kT k/e2 (23)
and Einstein relation:
D/μ = D/(σ/ne) = kT/e (24)
follow directly. μ is the mobility
The transport coefficients, and the relationships between them, are determined from the currents (equations (15)-(19)) calculated from Boltzmann transport equation (7).
5. Particles flow within a medium with a temperature gradient
The
particle flow may be that of a gas within a narrow pipe, a porous medium, or
that of atoms diffusing within a solid. The current of uncharged particles is,
(by (15)):
Jn = -[(4l/3)/(2πm)1/2] [d(n(kT)1/2)/dx] (25)
If there is no time dependent accumulation or depletion of particles the current will not depend on x and then the equation can be integrated to yield:
L Jn = [(4l/3)/(2πm)1/2] [nH(kTH)1/2 - nC(kTC)1/2] (26)
where L is the length of the medium, and the subscripts
C and H denote the cold and hot ends. If
the ideal gas law, p = n kT, is obeyed, then n (kT)1/2 can be replaced in equations
(25)-(26) by p/(kT)1/2. Another important
result is that the current is determined by the thermodynamic parameters at the
ends of the medium and not by their variations along it. In the special case
J = 0 the following expression becomes a system
invariant:
n (kT)1/2 = p/(kT)1/2 = Const (27)
In particular nC (kTC)1/2 = nH (kTH )1/2, and there is no dependence on the medium properties. This is Knudsen law (Knudsen (1952)).
6. Irreversible thermodynamics
Appendix-B, equations (64)-(83), summarizes equilibrium thermodynamics and some results that are applied here.
Consider the non-equilibrium system of section-2, figure-1, where the temperature and particle
density vary along the x-direction.
The system can be divided into sub-volumes ΔVi =
A Δxi
where A is the area cross-section.
If Δxi is equal to the mean free path then
local equilibrium thermodynamic functions may be used within each
volume ΔVi.
Assume that S(U, N) is the local entropy defined in a sub-volume.
The change of entropy ΔS within two neighboring sub-volumes,
i and i + 1, will be:
ΔSi = (∂S/∂U)i ΔUi + (∂S/∂N)i ΔNi (28)
ΔSi+ 1 = (∂S/∂U)i + 1 ΔUi+ 1 + (∂S/∂N)i+ 1 ΔNi+ 1 (29)
Since particles and energy flow from one sub volume to the other:
ΔUi+ 1 = -ΔUi = ΔU (30)
ΔNi+ 1 = -ΔNi = ΔN (31)
The entropy of the two sub volumes will be:
ΔS = ΔSi + ΔSi+ 1 = Δ(∂S/∂U) ΔU + Δ(∂S/∂N) ΔN (32)
Assuming that the entropy is locally not far from equilibrium, the equilibrium values conditions ∂S/∂U = 1/T and ∂S/∂N = -μ/T (equations (70)-(71)) may be applied.
ΔS = ΔU Δ(1/T) - ΔN Δ(μ/T) (33)
Dividing the local thermodynamic parameters and functions by the local volume ΔV yield their densities,
s = S/ΔV, u = U/ΔV, n = N/ΔV.
The parameter differences are replaced by their gradients,
in this example by the derivative along the x direction,
Δ(1/T) = l d(1/T)/dx, and
Δ(μ/T) = l d(μ/T)/dx. Finally, the time derivative of (33) yields:
d(Δs)/dt = l d(1/T)/dx d(Δu)/dt – l d(μ/T)/dx d(Δn)/dt (34)
If the local entropy is not far from equilibrium, the rate of entropy production may be expressed in terms of flows and forces:
d(Δs)/dt = Xu Ju + Xn Jn (35)
where, by comparison to (34), Ju = d(Δu)/dt, and Jn = d(Δn)/dt. The forces are:
Xu = d(1/T)/dx (36)
Xn = -d(μ/T)/dx (37)
The flows are related to the forces by linear phenomenological equations:
Jn = -L11 d(μ/T)/dx + L12 d(1/T)/dx (38 )
Ju = -L21 d(μ/T)/dx + L22 d(1/T)/dx (39 )
Onsager theorem postulates that the linear coefficients, Lij, are symmetrical: L12 = L21.
Inserting the chemical potential of mono-atomic ideal gas,
μ = -T ∂S/∂N =
kT ln[(T3/2/n)/(T03/2/n0)],
calculated in appendix-B equation (83), the derivative will be:
d(μ/T)/dx =
(3k/2) d(ln(T))/dx - k d(ln(n))/dx
= (3k/2T) dT/dx - (k/n) dn/dx
(40)
The flows will be:
Jn = L11 (k/n) dn/dx - [L11 (3k/2T) + L12 (1/T)2] (dT/dx) (41 )
Ju = L21 (k/n) dn/dx - [L21 (3k/2T) + L22 (1/T)2] (dT/dx) (42 )
The particle flow Jn and the energy flow Ju are coupled by cross terms with symmetrical linear coefficients. This result is how far irreversible thermodynamics takes us. It gives little information, if any, since the physics of the system is included in the explicit expressions of the Lijs that are not calculated by the theory.
However, the particle and energy currents (15)-(18), without external forces, given by Boltzmann's transport calculation,
with
A = [(4l/3)/(2πm)1/2], are:
Jn = -A [(kT)1/2 (dn/dx) + ((n/2)/(kT)1/2) d(kT)/dx] (43)
Ju = -2A [(kT)3/2 (dn/dx) + (3n/2) (kT)1/2 d(kT)/dx] (44)
These equations (43)-(44) do not contain unknown coefficients. Explicit values of the linear coefficients of irreversible thermodynamics may be calculated by comparing them to the similar flow equations (41)-(42):
L11 = -A (n/k) (kT)1/2 (45)
L12 = -2A (n/k) (kT)3/2 (46 )
L21 = -2A (n/k) (kT)3/2 (47 )
L22 = -6A (n/k) (kT)5/2 (48 )
The cross terms, L12 and L21, are equal, so that they verify Onsager's theorem.
7. Charge Transport through a junction
Electrons in solids occupy energy levels in pairs of opposite spins.
Lower levels are fully occupied and upper levels are empty, and the level population is
determined by Fermi-Dirac statistics. An electron may be scattered by a center within a medium only to
an empty level. For this reason low energy electrons are not scattered by the medium, since all the
nearby levels are occupied. Maxwell-Boltzmann velocity distribution is not applicable in this case.
Semiconductors are a special case. In these materials a fully occupied valence band is separated
from an empty conduction band by a forbidden gap without energy levels.
Doping the material with donors will introduce electrons to the conduction band and make it n-type.
Acceptors will introduce holes to the valence band and make it p-type. A donor atom has an
extra electron at a level just below the bottom of the conduction band. Thermal excitation
will transform it to the conduction band where it is free to move. An acceptor atom misses an electron
just above the valence band. Electron caught by the acceptor from the valence band will leave a hole
behind it that is free to move within the valence band. Practically, all donors are ionized so that the
electron-density is equal to the donor density. Similarly, the hole-density is equal to the acceptor density.
Maxwell-Boltzmann velocity distribution may apply to semiconductors where the charge density,
either electrons or holes, is lower than the energy level density.
Consider two pieces of a semiconductor with higher nL and lower
nR electron densities.
The left is n-type where nL is equal to the donor density.
The right may be n-type or p-type. For p-type
material nR is determined by the condition
pR nR = p n = Const,
that is general to semiconductors. pR is equal to the acceptor density.
If the two pieces are brought into contact to form a junction, electrons will start to flow from
the left nL side to the right
nR side.
This flow generates space charge region, electric field,
and potential difference Vc between the
two pieces that stop further electron flow. Vc is
the contact potential. It is not directly measureable by a voltmeter, for example, because the voltmeter
probes make their own contact potentials with the two ends of the junction. The sum of all junction potentials is then zero.
If the two pieces are separated after being in contact, their capacity will drop, the voltage on
them will grow and it will be possible to measure it. Methods that measure the contact potential are based on this phenomenon.
It is assumed that the junction is perpendicular to the x-direction, and that the depth of the space charge layer in it is
small compared to the electron's mean free path. The thermal velocity of electrons at the left side must
have a minimal component vx in
order to overcome the potential barrier and cross to the right side:
(1/2) m vx2 > eVc.
Electrons at the right side do not have any barrier for crossing back to the left.
An electron that crosses the junction from left to right, will be slowed down by the electric field
and lose the energy eVc. This energy will be thermally
regained from its vicinity. An electron moving the opposite way will be accelerated by the field
and thermally deliver the field-gained energy to its vicinity.
For this case Boltzmann transport equation f
is approximated by the first non zero term in equation (7), which is
the equilibrium distribution f0.
The current, equation (8),through the contact will be:
Jn = ∫(vx > v0) f0(v) vx d3v + ∫(vx < 0) f0(v) vx d3v = Jn1 –Jn2 (49)
where: v0 =(2 eVc / m)1/2.
It is convenient to use here Cartesian coordinates
d3v = dvx
dvy dvz.
By inserting Maxwell-Boltzmann distribution, equation-(12) , for f0 :
Jn1 = nL (m /2πkT)3/2
0∫∞ e-αz dvz
0∫∞ e-αy dvy
v0∫∞ e-αx vx dvx
(50)
Jn2 = nR (m /2πkT)3/2
-∞∫0 e-αz dvz
-∞∫0 e-αy dvy
-∞∫0 e-αx vx dvx
(51)
where: αi = mvi2 / (2kT), i = x, y, z.
Using the formulas, appendix-A, (a > 0):
0∫∞ e-(a x^2) dx = (π/a)1/2/2 (52)
and
0∫∞ e-(a x^2) x dx = 1/(2a) (53)
the integrals will be:
0∫∞ e-αi dvi = (πkT/m)1/2
(54)
v0∫∞ e-αx vx
dvx = (kT/m) e-eVc/ kT
(55)
-∞∫0 e-αx vx
dvx = (kT/m)
(56)
And the overall current:
Jn = Jn1 – Jn2 = (kT/8πm)1/2 nL (e-eVc/kT – nR/nL) (57)
Since the system is at equilibrium, Jn = 0, the potential difference at the contact will be:
e-eVc/kT = nR/nL (58)
or:
Vc = (kT/e) ln(nL/nR) (59)
If an external voltage source V is connected to the system, and the voltage falls on the junction, the current will be:
Jn = (kT/8πm)1/2 nL (ee(V – Vc)/kT – nR/nL) (60)
Or, by (58):
Jn = (kT/8πm)1/2 nR (eeV/kT – 1) (61)
This formula is the I–V diode equation.
8. Thermoelectric effects
Thomson effect: Generation or absorption of heat in a current carrying conductor.
Generation or absorption of heat along a conductor is given by the derivative of the energy current,
Ju = 2kT Jn - 2((4l/3)/(2πm)1/2)
n (kT)1/2 d(kT)/dx
,
equation-(18), with respect to
x.
Assuming that the particle flow does not depend on x,
dJn/dx = 0, and assuming also
that the temperature change is linear with the distance, d(kT)/dx = Const,
the heat generation or absorption will be:
dJu/dx = [2 Jn -((4l/3)/(2πm)1/2) n / (kT)1/2] d(kT)/dx (62)
Peltier effect: Heating or cooling a junction by electric current.
An electron that crosses a junction will be either slowed down, or accelerated by a contact potentiall difference
Vc, depending on its polarity.
Thus, it will absorb or deliver an amount of heat e Vc to the junction.
Vc is given by
Vc = (kT/e) ln(nL/nR),
equation (59).
Seebeck effect:
Direct power generation from temperature difference.
Direct conversion of thermal energy to electrical energy by a junction is discussed
by applying the original Carnot method to a junction device operating in a reversible closed cycle.
The "Carnot machine" shown in figure-2 has some resemblance to devices
that are used to measure contact potentials (Klein et al (2003)).
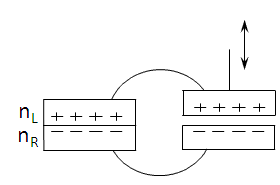
Figure-2: A "Carnot machine" comprises of two junctions connected in parallel. One with two semiconductors in permanent
contact, and one with the two parts separable. The distance between them is externally controlled.
Two junctions are connected in parallel. In the left junction two semiconductors are in permanent contact while in the
right junction they are separable and the distance between them is externally controlled.
The connecting wires are made of the same semiconductor material so that there is only one contact junction in the device.
The contact potential difference within the junction is given by
Vc = (kT/e) ln(nL/nR),
equation-(59).
However, there is no external voltage difference between the junction ends.
Since the junction parts are electrically charged, there will be attraction force between them. Distance change
between the separated parts requires mechanical work.
The machine operates in a four step cycle between a hotter heat-bath TH
and a colder heat-bath TC.
In step-1 the machine is attached to the hot bath TH
and the distance between the two parts of the right junction
is reduced by moving the upper part down. The junction potential VH
does not change during this isothermal movement and the increasing capacity of the right junction
drives charge flow Δq in the two junction circuit.
The flow through the left junction absorbs heat
Δq VH
from the hot bath (Peltier effect), and the right junction performs
an equivalent work on the external force that holds it in place.
In step-2 the upper part of the right junction continues to move down while
the machine is separated from the hot bath TH.
During this adiabatic step the machine cools down and the movement continues
until it reaches the temperature TC of the cold bath,
while the junction potential decreases from VH
to VC.
In step-3 the machine is attached to the cold bath TC and
the distance between the parts of the right junction
is increased by moving the upper part back up. The junction potential VC
does not change during this isothermal movement and the decreasing capacity of the right junction
drives charge flow Δq in the opposite direction to step-1.
The flow through the left junction delivers heat Δq VC
to the cold bath (Peltier effect the other way) and the external force performs
an equivalent work on the right junction.
In step-4 the upper part of the right junction continues to move up while
the machine is separated from the cold bath TC.
During this step the machine heats up and the adiabatic movement continues
until it reaches the temperature TH of the hot bath.
The junction potential increases from VC
to VH and the machine completes the cycle and returns to its original state.
The adiabatic work done by the machine on the external force in step-2 is equal to the adiabatic work
done by the external force on the machine in step-4. The electro-motive force V of
the machine is the work done by moving a unit charge in a complete closed cycle. This work is equal to the sum of
of step-1 and step-3 for a unit charge e.
Using
Vc = (kT/e) ln(nL/nR),
equation (59), this work is equal to:
eV = k(TH - TC) ln(nL/nR) (63)
Combining equations (59) and (63) yields Carnot's efficiency 1 - TC / TH.
9. Summary and conclusions
Boltzmann transport equation relates
the properties of a non-equilibrium system, expressed by a non-equilibrium
distribution, in terms of local equilibrium distributions. The equation is
derived by assuming random movement of particles within a medium.
Boltzmann transport equation is applied to calculation of the general currents in a medium with particle and temperature gradients. The currents determine the transport coefficients of the medium.
The calculated diffusivity, electrical and thermal conductivities verify Wiedemann-Franz and Einstein Laws.
The calculated current of uncharged particles verifies Knudsen law.
See:
Expansion of an Ideal Gas
Osmosis and Thermodynamics
van't Hoff's Evidence
Appendix A: integrals
0∫ ∞xn
exp(-a2x2)
dx = Γ((n+1)/2) / 2an+1
Γ is the gamma function:
Γ(n) = (n – 1)!
Γ(x + 1) = x Γ(x)
Γ(x)
Γ(x + 1/2) = Γ(2x)
π1/2 / 22x - 1
Γ(1/2) = π1/2
Γ(3/2) = (1/2) π1/2
Γ(5/2) = (3/4) π1/2
Appendix B: Summary of equilibrium thermodynamics
Each state of a quantum system is assumed to have the same probability. Ω(U)
is the system's density of states as a function
of the energy U, and the entropy is:
S(U) = k ln(Ω(U)) (64)
where k is Boltzmann's constant. The entropy is maximal when the system is
at thermodynamic equilibrium.
The temperature is:
1/T = dS(U)/dU (65)
x is a parameter of the system, volume, number of particles, etc.,
and its conjugate force X is:
δU = -X δx (66)
The first law of thermodynamics, for a system in thermal contact with a heat bath, of a temperature
T, is:
δU = δQ – Σi Xi δxi = δQ – pδV + μδN + … (67)
where the volume V, the number of particles N, ... are
parameters of the system, the pressure p, the chemical potential
μ, ... are their conjugate forces, and δQ is
the heat flow from the heat bath. The first law is conservation of energy.
The overall entropy S*, for a system at equilibrium with a heat bath,
is the sum of the system entropy S(U, xi)
and the bath entropy ST(UT).
S* = S(U, xi) + ST(UT) (68)
The maximum condition for the entropy is:
0 = dS* = (∂S/∂U) dU + Σi (∂S/∂xi) dxi +
(∂ST/∂UT) dUT
= (∂S/∂U) dU + Σi (∂S/∂xi) dxi +
(∂ST/∂UT) (-dU – Σi
Xi dxi)
= [(∂S/∂U) – (∂ST/∂UT)] dU + Σi
[(∂S/∂xi) – (∂ST/∂UT) Xi] dxi
(69)
Therefore, the conditions for thermodynamic equilibrium are:
(∂S/∂U) = (∂ST/∂UT) = 1/T (70)
(∂S/∂xi) = Xi/T (71)
Reversible process
When a parameter change δx is slow enough the system will smoothly
adjust its equilibrium state to it. If the change δx is reversed
the system will reverse its response and return to its original state.
A process that at any moment can reverse its direction, in response to reverse of a parameter
change, is a reversible process.
The energy conservation for an equilibrium system in contact with a heat bath is, by (67):
δQ = δU + Σi Xi δxi (72)
δQ is the heat supplied from the bath. Using the equilibrium conditions (70), (71):
δS = (∂S/∂U) δU + Σi (∂S/∂xi) δxi = (1/T) δU + Σi (Xi/T) δxi = δQ/T (73)
or
δS = (1/T) δU + (p/T) δV - (μ/T)δN + ... = δQ/T (74)
The equation δS = δQ/T is the classical definition of entropy.
The overall entropy change in a reversible process is zero, ΔSoverall = 0. If a system is thermally isolated from its vicinity, then the process is adiabatic and the entropy change of the system is zero, ΔSsystem = 0. If a system is in thermal contact with a heat bath, then the process is isothermal and the sum entropy change of the system and the bath is zero, ΔSsystem + ΔSbath = 0. Entropy change between two states of a system may be calculated by following a reversible path between them.
Entropy change in ideal gas
A system is defined by three parameters out of four, the pressure p,
number of particles N,
volume V, and the temperature T.
These parameters are connected by the ideal gas
equation: p V = N kT.
A standard system is similarly defined by three parameters out
of p0, N0,
V0,
and T0, where p0 V0
= N0 kT0.
n = N/V is the particle density.
The entropy change is calculated for moving ΔN particles, by a reversible process,
from a standard system (p0, N0,
V0, T0)
to a specific system (p, N,
V, T)
Consider the standard system (p0, N0,
V0, T0),
in contact with a heat bath. One wall of the system has a small hole in it, and there is a moving partition
that encloses an additional volume ΔV0.
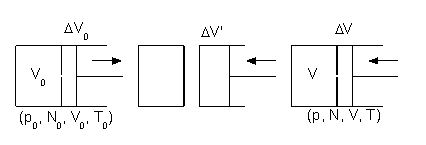
Figure 3: Entropy of an ideal gas.
The partition is first attached to the wall with the hole, so that the initial volume ΔV0 is zero. The partition then separates from the wall, moves and increases the volume ΔV0 to some small value, and removes ΔN particles from the system. If ΔV0 is much smaller than the volume V0, ΔV0 << V0, then the gas pressure p0 will almost not change during the movement. The isothermal work of pushing the partition by the gas is W1 = p0 ΔV0. The energy for this process, ΔQ1, comes from the heat bath:
ΔQ1 = W1 = p0 ΔV0 = ΔN kT0 (75)
The entropy change for this process is:
ΔS1 = ΔQ1/T0 = ΔN k (76)
The hole is now closed. ΔV0 is separated
from the volume V0
and is isolated from its vicinity. Now the partition reverses direction,
compresses the gas and heats it adiabatically to the temperature T and
pressure p’. During this process there is no entropy change.
The pressure increase in
adiabatic compression of mono-atomic ideal gas, is (Appendix C):
p’ = p0 (T/T0)5/2 (77)
The volume ΔV’ is now connected to a heat
bath of a temperature T
and the partition continues to compress it to a
volume ΔV until the pressure
reaches p.
The isothermal work done during this process is:
W2 = p’∫pp dV = ΔN kT p’∫pdp/p = ΔN kT ln(p/p’) (78)
And the entropy change is (by (77)):
ΔS2 = ΔQ2/T = ΔN k ln[(p/p0) (T0/T)5/2] (79)
The volume ΔV is connected now through a hole to the system
(p, N, V, T)
and the partition pushes the ΔN particles into it by reducing
ΔV to zero .
The isothermal work for this last process is:
W3 = p ΔV = ΔN kT (80)
and the entropy change is:
ΔS3 = ΔQ3/T = -ΔN k (81)
The overall entropy change, during these three processes, is:
ΔS = ΔS1 + ΔS2
+ ΔS3 = ΔS2,
since ΔS3 = - ΔS1.
Therefore:
ΔS = ΔN k ln[(p/p0)
(T0/T)5/2]
= ΔN k ln((n/n0) (T0/T)3/2)
= ΔN k ln[(n/T3/2)/(n0/T03/2)]
(82)
The chemical potential is (by (71), (74), (82)):
μ = -T ∂S/∂N = kT ln[(T3/2/n)/(T03/2/n0)] (83)
Appedix-C: Adiabatic expansion of a mono-atomic ideal gas
The gas pressure
A particle in a box of volume V moves with a velocity
v at an angle φ to the
perpendicular of a wall as shown in figure-4.
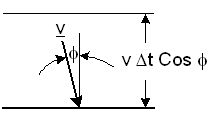
Figure-4: Elastic collision of a particle with a wall.
It will collide with the wall during a time Δt, if its distance from the wall is less than |v| Cosφ Δt. The number ΔNcol of particle collisions with a unit area of the wall during Δt is:
Δ
Ncol = [n ∫f0(v) |v| Cosφ d3v] Δt (84)n is the particle density, f0(v)
is the probability that the particle velocity is
v, normalized by
∫4π
v2 f0(v) dv = 1, and
d3v = 2π
v2 dv Sinφ dφ
. Substituting in equation (84):
ΔNcol = n (∫2π v2 f0(v) v dv) (∫Cosφ Sinφ dφ) Δt (85)
The three-dimensional average velocity of particles is
<v> =∫4π
v2 f0(v) v dv. <v> is not zero since the integration is
only over positive values. The trigonometric integral over half the sphere is
∫Cosφ
Sinφ dφ
= 1, ( 0 < φ < π/2),
therefore:
ΔNcol = n (<v>/2) Δt (86)
Upon a collision with the wall the particle will transfer a momentum 2mv Cosφ to the wall. The overall momentum ΔM, delivered to a unit area of the wall during Δt, is the sum of momenta delivered by all the colliding particles that come from all directions of the half sphere. Similarly to equations (84) - (85):
ΔM = n 2m (∫2π v2 f0(v) v2 dv) (∫Cos2φ Sinφ dφ) Δt (87)
The three-dimensional average is
<v2> =∫4π
v2 f0(v) v2 dv,
∫Cos2φ
Sinφ dφ = 1/3, and the pressure
p =ΔM /
Δt is therefore:
p = n m <v2>/3 (88)
The thermal average is calculated by applying Maxwell-Boltzmann distribution:
f0(v) = (m / 2πkT)3 / 2 exp(-mv2 / 2kT) (89)
to the calculation of <v> and <v2> (appendix A):
<v> = 4π ∫f0(v) v3dv = 2 (2kT / πm)1/2 (90)
<v2> = 4π ∫f0(v) v4 dv = 3kT / m (91)
Substituting <v2> in equation (88) yields the pressure:
p = n kT (92)
Equation (92) is the state equation of an ideal gas.
Adiabatic expansion of a mono-atomic ideal gas
In adiabatic system the particles do not exchange energy with the walls by inelastic collisions and the only energy transfer
mechanism is via elastic collisions with a moving partition.
A single particle in a box of volume V and of unit cross section,
with one wall a moving partition, collides
ΔNcol / N
= (v/2) Δt / V times with it
during a time Δt (equation (86)).
Since the relative velocity between the particle and the moving partition is conserved, during
each collision the particle will lose (or gain) a velocity 2vM,
twice the partition velocity. A partition
that moves in the x-direction will change the vx component
of the particle velocity. However, the velocity change will eventually spread to the
vy and vz components.
Therefore, the change of a particle velocity during
Δt will be:
dv = -(1/3) 2vM (v/2)
Δt / V = -(v/3) dV/V (93)since vMΔt = dV. The equation of adiabatic expansion of a mono-atomic gas, without internal degrees of freedom of gas particles, is calculated by integration of equation (93):
v/v0 = (V0/V)1/3 (94)
and by equation (88):
p/p0 = (V0/V)5/3
or, by the state equation (92), p = n kT:
T/T0 = (V0/V)2/3 or p/p0 = (T/T0)5/2 (95)
Since:
d(T/T0) = (-2/3) (V/V0)-5/3 d(V/V0)) (96)
the work of adiabatic compression or expansion of the gas will be:
W = 0∫V pdV =
p0V0 0∫V(V/V0)-(5/3)
d(V/V0)
= (3/2) p0V0 0∫T d(T/T0)
= (3/2) (p0V0/T0)
(T - T0) = (3/2) N k (T - T0)
(97)
References
C. Kittel, Elementary Statistical Physics (Wiley, New
York, 1958) pp. 159-165, 192-201.
M. Knudsen, Kinetic Theory of Gases,
(Methuen, London, 1952) pp.33-34.
F.W. Sears, G.L. Salinger,
Thermodynamics, Kinetic Theory, and Statistical Thermodynamics (Addison-Wesley,
3rd ed 1975) pp 331-336, 355-361.
J.M. Ziman, Principles of the Theory of
Solids (Cambridge University Press, 1969) pp 116-123, 179-200.
U Klein, W Vollmann, P Jose Abatti, Contact Potential Differences Measurement:
Short History and Experimental Setup for Classroom Demonstration,
IEEE Trans. Education, Vol. 46, No. 3 (2003) pp 338-344.
On the net: May, 2002. Irreversible thermodynamics added: October 2011.
Charge Transport through a junction and thermoelectric effects added: September 2012.
Scattering of Directional Light
Scattering of Directional Light
By the author:
- "Thermoelectric Effects Peltier Seebeck and Thomson",
Abstract: http://urila.tripod.com/Thermoelectric_abstract.htm
Full page: http://urila.tripod.com/Thermoelectric.pdf, February 2014. - "Osmosis Desalination and Carnot", http://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
- "Light Scattering", http://urila.tripod.com/scatter.htm, August (2011).
- "The Sun and the Moon a Riddle in the Sky", http://urila.tripod.com/moon.htm, July (2011).
- "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
- "van't Hoff's Evidence", http://urila.tripod.com/evidence.htm, October (2007).
- "Osmosis and Thermodynamics", http://urila.tripod.com/osmotic.htm, January (2007).
- "Expansion of an ideal gas", http://urila.tripod.com/expand.htm, December (2002).
- "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", http://urila.tripod.com/Seawater.htm, May (2002).
- "Boltzmann Transport Equation", http://urila.tripod.com/Boltzmann.htm, May (2002).
- "Energy of Seawater Desalination", http://urila.tripod.com/desalination.htm, April (2000).
- "Avogadro's number atomic and molecular weight", http://urila.tripod.com/mole.htm, April (2000).
- "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", http://urila.tripod.com/colligative.htm, December (1998).
- "Osmosis Reverse Osmosis and Osmotic Pressure what they are", http://urila.tripod.com/index.htm, February (1998).
- "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
- "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).
Links:
- Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
- Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
- The Blind Men and the Elephant
- My Spin on Lunacy
- Five Weeks in a Balloon
- The first man I saw
- "Faster, Faster!"
- Perfection can't be rushed
- The man higher up
- Brains
- The First-Class Passenger
- other