Osmosis Desalination and Carnot

Figure-1: A stretched rubber band – an example of a reversible process. Increasing the force will lengthen the band. Reducing the force to its previous value will shorten the band to its previous length.


        Not all processes are reversible, for example mixing a spoon full of sugar in a tea cup. The sugar can't be "unmixed" afterwards from the tea by reversing the spoon movement. Sugar mixing is an irreversible process.

        Carnot postulated that reversible processes are the most efficient possible in nature. Every process which is not reversible will be less efficient. This simple postulate has, as we will see, far reaching implications, and Carnot used it to analyze the operation of the steam engine. The operation of the steam engine is a complicated process that includes steps of heating and cooling, and Carnot had to deal with a full cycle of operations, some of them with increasing or decreasing temperature. Our desalination system is simpler and it is possible to assume that the temperature is uniform and constant.

        Now, that we are equipped with this strong law of Carnot it is time to go on to water desalination. Figure-2 shows a vessel built of a U shaped pipe with a semi-permeable membrane at its bottom that separates its two arms. A semi-permeable membrane is a membrane that allows passage of water through it but blocks the passage of salts.

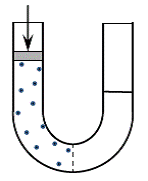
Figure-2: A semi-permeable membrane separates the arms of a U shaped pipe that contains water. Salt in the left arm generates osmotic pressure in it. The pressure on a piston above the solution at the left arm determines the direction of water flow through the membrane.


        Water is first added to the vessel and since it can pass from side to side it will reach the same level on both arms. Now, some salt is added to the left arm. The salt that cannot pass to the other arm dissolves in the water and generates osmotic pressure which induces water flow from the pure water arm to the salt solution arm. The water passage elevates the solution level above the pure water level. This process of water passage is called osmosis. Why is osmotic pressure generated? And why does it induce water passage? On purpose we will reserve these questions to a later discussion.

        It is possible to stop the passage of water from arm to arm by putting a piston on the solution face and generating pressure on it that is equal to the osmotic pressure. Now the system is in a static state, nothing moves. If we increase the pressure on the piston it will move down and water will flow back from the salt solution to the pure water. This is reverse osmosis and the process is desalination since we transferred water from a salt solution to pure water. If we reduce the pressure on the piston back to its initial value, the direction of water flow will reverse again, water will pass to the salt solution and the piston will move up and return to its initial position. What is this process? Right, it is a reversible process. What does Carnot's law tells us about it? It is the most possibly efficient.

        When the piston pushes a volume V of water through the membrane then the work performed is equal to the osmotic pressure times this volume. So that we know how much energy should be invested in order to desalinate a given quantity of water. This energy is the minimal required for desalination because the process is reversible. In any other process that is not reversible we will have to invest more energy.

        The energy invested in pushing the piston downwards is exactly equal to the energy returned when the piston is restored to its original position. This description seems too good to be true and indeed, there are losses during each stage that cannot be avoided. For example, water passage through the membrane involves unavoidable energy loss that does not depend on the direction of water flow. Pushing down the piston requires more energy than that of the reversible limit, and when it is pushed back up less energy than the reversible limit is gained. Energy is lost both ways. It is possible only to reduce it by decreasing the rate of water flow. A reversible process is therefore, an abstraction or a limit of a natural process that always involves some irreversible loss.

        From these considerations it is clear that it is not possible to desalinate water without energy investment at all. If in some magical way we were to succeed to desalinate water from a solution without any energy input, we could take this water and produce energy with our vessel by returning the water to the salt solution with the osmosis process. By repeating this procedure over and over we obtain a perpetuum mobile machine that produces energy from nothing. Such a process is of course not possible.

        As an intermediate summary, there is a process of osmosis and reverse osmosis that virtually we know nothing about, nevertheless, with the help of Carnot's law we know about it a whole lot.

        Before Carnot the view of the material world was based on the mechanics of Newton's laws. Newton's laws are deterministic. According to them, if the state of a system is known, i.e., the positions and velocities of all the particles in the system, then the laws precisely determine the places where the particles will be at any time in the future. Similarly, the laws determine the places and velocities where they have been at any time in the past. In fact, knowing, not knowing, is not that important. The laws act on the particles anyway. This deterministic view of the world, which is in contrast to our everyday experience, was a great puzzle for a long time.

        The mechanical view of the world led people to seek the very details of systems in order to apply Newton's laws on them and to understand them by this way - and more details the better. In contrast to that, the use of Carnot's law in our modest example of osmosis enables understanding matters of importance in a system that we are almost not familiar with and that we do not understand. In many cases, the detailed knowledge, which is required in the mechanical view, is unnecessary. Carnot's law extends the idea of what science is all about. If prior to Carnot only mathematics, physics, astronomy, and maybe a little chemistry, were considered sciences, Carnot's law opened a wide gate to go through for the life sciences, economics and social sciences, as well as arts and humanities. Matters of systems may be discussed meaningfully even if very little is known about them.

        The apparently naive postulate of Carnot, that a process which is not reversible will be always less efficient than a reversible process, has even more important implications. Suppose that we film a process which is not reversible with a video camera. At some moment we stop and run the film backwards, like what we see many times on television or in the movies. Is the backward film, which we look at, a possible process in nature? According to Newton, yes. All we have to do is to stop the system and to reverse the direction of all the particles backwards. All the particles will then move back to their initial places and the system will return to its initial state, just as seen in the reversed film. What does Carnot's law say about it? Not at all. Why? Because if the efficiency of the originally filmed process is below that of a reversible process, then the efficiency of the backward run process, that returns the system to its initial state, will be higher than that of a reversible process. This is not possible in nature according to Carnot's law. Who is right? Newton or Carnot? Reality tells us that Carnot is right. Newton's laws are not capable of distinguishing between past and future. In contrast, this property of Carnot's law, that it is not possible to reverse processes in nature back in time, means that there is a difference between past and future. Therefore, there is something new in Carnot's law that does not exist in Newton's laws. It took long for this point to be comprehended.

        The pioneering work of Carnot, some people say "enlightenment", led the way to the science of thermodynamics. The ability to deal with systems when not much is known about them, led to introduction of probability into the theory, and out of that to the science of Statistical Mechanics. Quantum theory, developed during the first part of the 20th century, replaced "don't know" by "cannot know", and by that the conflict with the deterministic Newton's laws disappeared to a large extent. Thermodynamics and statistical mechanics have since penetrated into the basis of all branches of science and it seems impossible to do without them. For example the "black holes", these strange bodies in the universe that absorb anything nearby them. Thermodynamic arguments of the last years indicate that also these bodies evaporate slowly and lose their material until they disappear.

        After wandering at such heights it is time to land on firm ground and to return to water desalination. We may remember the kilo-calorie from school days, the energy unit that is equal to the amount of heat required to heat a liter of water by one degree Celsius. In order to heat one liter from a temperature of 20 degrees to boiling temperature of 100 degrees, we need, therefore 80 kilo-calories. If we want to boil this water and to transform it from a liquid to a vapor we will need more 540 kilo-calories. How many kilo-calories are required in order to desalinate one liter of sea-water? The minimal energy, by Carnot's law, is a little more than half a kilo-calorie. In desalination plants there are unavoidable losses and the actually required energy is about 2 to 3 kilo-calories. Even so, the energy required to heat water for a cup of coffee is far above the energy required to desalinate this water.

        Desalination requires energy no doubt, but it is certainly not energy intensive, and since there is a great water shortage in many places in the world, that will become only more severe, there is no other way but to apply it. Heating water is much more energy intensive. During the 1960's of the last century a law was passed that required every new apartment to have a solar water heater. During the years this law resulted in significant saving of fuel and energy. It would be interesting to know how much was saved since then.

        Some places, like Scandinavia and Siberia, have excess of pure water. In these places it is possible to produce energy by osmosis from the salinity of seawater. A special case is the dead-sea which is about ten times more saline than seawater. For decades the water of the Jordan-River has been pumped up from the Lake of Galilee and used for drinking and irrigation. If the river water would be allowed to flow again to the Dead-Sea, as in the past, then it would be possible to produce energy where the river flows into the sea. Much more energy may be produced since the water is much more saline. A full size desalination plant may supply similar amount of water and, at the same time, the Dead-Sea could be saved from evaporating and eventually disappearing.

        There is one debt left. What is actually osmosis?

        The explanation to the phenomenon of osmosis was given by vant-Hoff, a Dutch chemist, and it won him the first Noble prize in chemistry in the year 1901. van't-Hoff made an analogy between particles in a solution and molecules in a container, and postulated that the osmotic pressure formula in a solution is identical with the pressure formula of ideal gas in a container. The analogy infers that the osmotic pressure does not depend on the type of the dissolved particles, but only proportional to their concentration.

        van't-Hoff writes: "The mechanism by which, according to our present conceptions, the elastic pressure of gases is produced is essentially the same as that which gives rise to osmotic pressure in solutions. It depends, in the first case, upon the impact of the gas molecules against the wall of the vessel; in the latter, upon the impact of the molecules of the dissolved substance against the semipermeable membrane, since the molecules of the solvent, being present upon both sides of the membrane through which they pass, do not enter into consideration."

        van't-Hoff was also the first to suggest a spatial three dimensional structure for a chemical molecule, and by this suggestion he opened new horizons to the science of chemistry and all that followed. In historical perspective this work might worth a Nobel prize as well. van't-Hoff thought of the three dimensional structure when he was a PhD student, but someone advised him not to publish it immediately, but to wait and submit a more standard work for the degree, and so he did.

        Luckily for van't-Hoff the experimental data on osmosis were not clear enough, and so he could pass his theory. It was soon found out that the osmotic pressure formula works in molecules like sugar, but even with a simple molecule like table salt the osmotic pressure is about twice as much as that calculated from the formula.

        This result brought Arrhenius, a Swedish chemist, to suggest that a molecule of table salt disintegrates to ions of sodium and chlorine when it dissolves in water. Since each salt molecule is composed of these two ions, their overall concentration is double that of the molecular concentration. Therefore, the osmotic pressure should also be doubled. Arrhenius didn't receive an advice similar to that given to van't-Hoff, and he submitted this theory for his PhD. His examining professors didn't believe him but were afraid to disqualify his work. So they gave it a low passing grade. Arrhenius became well known with the coming years, contributed more important scientific achievements, and received a Nobel-prize in 1903.

        van't-hoff's analogy between osmotic pressure and gas pressure was not accepted with the years that followed. Many opponents rejected it, and it is not accepted even today. There were and are people that claim that the similarity between osmotic pressure and gas pressure is just a coincidence. There is not much benefit discussing this matter, and what remains is to cite some of the greatest people of science.

        A young and not yet well known man, Albert Einstein, a third degree patent examiner in the patent office of Bern, wrote five scientific works in 1905 that changed the world, and this year became known as "annus mirabilis" – the year of wonders. His second work deals with "Brownian movement". Brown was a botanist who looked through the microscope at tiny particles that float in a drop of water. The particles were not at rest, but constantly vibrated and moved from place to place in a random manner. At first the phenomenon was attributed to live bodies, but then it turned out that it was observed in inanimate particles. Einstein explained this phenomenon by proposing that the liquid molecules, that surround the particle, hit it continuously from all directions and by that they force it to move randomly.

        Why this explanation is important? Everybody knows that materials are composed of atoms that once were considered basic indivisible particles. Today we know that an atom consists of a nucleus made of protons and neutrons that is surrounded by electrons. These particles are built of even more fundamental particles. During the 19th century the atomic hypothesis was not taken for granted and many people thought that atoms do not really exist, but are just a mathematical convenience that helps performing calculations. After the publication of Einstein's work the idea that atoms really exist became generally accepted.

        At the beginning of his work Einstein writes (the source is in German): "We must assume that the suspended particles perform an irregular movement - even if a very slow one - in the liquid, on account of the molecular movement of the liquid; if they are prevented from leaving the volume V* by the partition, they will exert a pressure on the partition just like molecules in solution." [3]. (the partition is the semi-permeable membrane).

        Enrico Fermi, one of the important contributors to the development of quantum theory and to nuclear physics, and who also built the first nuclear reactor, wrote a book entitled "Thermodynamics". The book won praises for his depth of thought and clarity of presentation, and it seems that very few read it. Here is a short paragraph from the discussion of osmosis: "Then the pressure on the side of the membrane facing the solution will be increased by the impacts against it of the molecules of the dissolved substances," [4].

        The citations speak for themselves. The writer of these pages thinks that the osmotic pressure is essential to maintain the balance of linear momentum on the solution. This is more or less what Einstein and Fermi say.

        Why the water molecules can penetrate through the semi-permeable membrane? The writer looked for an explanation but didn't find any. He assumes that the permeable membrane contains hydrophilic sites that attract water, and the water molecules hop from site to site, and in this way pass through the membrane.

        In summary, reflections on the meaning of science, and on science and the world, may come from the "big bang" and from the "god particle", and also from matters of plumbing.

References:

1. S. Carnot, "Reflections on the Motive Power of Fire", Dover Publications, Inc., New York (1960, 1988)
2. J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen", Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
   J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
   translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888)
   J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
   in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
   translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42
3. A. Einstein, "On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat", Originally published in Annalen der Physik 17 [1905]: 549-560
   A. Einstein, "Investigations on the Theory of the Brownian Movement", translated by A.D. Cowper, Dover Publications, Inc., New York, pp. 1-18 (1956)
4. E. Fermi, "Thermodynamics", Dover Publications, Inc., New York (1936, 1957) pp. 118-123

On the net: December 2012.

By the author:

1. Osmosis Desalination and Carnot, https://urila.tripod.com/Osmosis_Carnot.htm, December (2012).
2. Osmosis Desalination and Carnot, https://urila.tripod.com/Osmosis_Carnot.pdf, December (2012).
3. "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
4. "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
5. "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
6. "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
7. "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
8. "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
9. "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
10. "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
11. "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
12. "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
13. "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
14. "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.pdf, December (1998).
15. "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
16. "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
17. "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).

Links:

1. Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
2. Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
3. The Blind Men and the Elephant
4. My Spin on Lunacy
5. Five Weeks in a Balloon
6. The first man I saw
7. "Faster, Faster!"
8. Perfection can't be rushed
9. The man higher up
10. Brains
11. The First-Class Passenger
12. other