Blue Marble the Uniform Earth Image

Abstract
"Blue Marble", the full earth image, is uniform as well as all the other full planet images and their moons. The uniformity is due to a single event scattering of sunlight. Single event scattered light is coherent and leads to enhanced backscattering of light, the opposition effect. Coherent backscattered light is separable from non-coherent light by interferometry. It increases the observation distance of celestial bodies, asteroids, and the penetration of image observation within scattering media.

Introduction
The term "blue marble" was coined by NASA to the full earth image taken by the Apollo 17 team in 1972 ¹. The first similar full earth image was taken earlier in the DODGE (Department of Defense Gravity Experiment) in 1967 ². Images are now available routinely since 2015 from the Deep Space Climate Observatory located about 1.6*10⁶ km from the earth ³.

Figure-1: The Blue Marble, full earth image taken by the Apollo-17 team ¹.

According to Lambert's cosine law ⁴, the intensity of such images should be maximal at the image center, and fade to zero at the periphery by the cosine function. However, all these images have a common feature, starting from the first DODGE image to the present day images: The average image density is uniform from the face center of the image towards its periphery. More than that: The earth image includes large areas of gas phase – clouds, liquid phase – oceans, and solid phase – land, and the uniformity is nearly true for each phase separately. This feature is not discussed in the literature, not even mentioned in it.

The uniformity is not unique to the earth, but it is also observed in all the other planets and planet moons when they are back illuminated by the sun, that is, the image is 180 degrees backward scattered from the object toward the observer ⁵.

Light reflection from a material is considered in the literature either specular, mirror like, or diffusive. Specular reflection obeys the mirror law, while diffusive light scattering spreads in all direction. Random diffusive scattering is considered a multiple scattering event ⁶ and it must obey Lambert's scattering law ⁴: The scattering intensity is maximal in a perpendicular direction to the surface of the scattering body. It falls off according to the cosine function when the scattering angle deviates from perpendicular.

In the case of a sphere, backward scattering, scattering 180 degrees back, is maximal at the center of the sphere. It falls to zero according to the cosine function when advancing from the sphere surface center toward to its periphery. Bodies that their images comply with Lambert's cosine law are considered Lambertian scatterers ^{7, 8}.

The uniform back scattered images, of all the planets and their moons ⁵, show that they are not Lambertian. There are thousands upon thousands of such images but not a single true photo that complies with the cosine law. The only images that do comply with the law are rendered, images that are at least partly simulated.

The earth's moon, our own moon, is the only body where the full image was studied in detail and theories have been suggested for the image uniformity. There are reviews of the subject including detailed reference lists ^9-10. The hither to theories of light scattering from the moon face involve specific properties of the surface material, rocks and dust. They are not applicable to the earth image where the uniformity is observed separately in the air, sea, and land. It is more likely that a single theory should be applicable to the moon, earth, and all other cases.

Discussion

Going a little into the scattering mechanism may shed light on the observed earth images.

Light that travels within a material polarizes its matter. The electromagnetic radiation stimulates electric dipole oscillations within it, and each dipole becomes a source of electromagnetic radiation. Each dipole oscillates with a phase that is determined by its position in space, and its radiation field adds by vector addition to the stimulating radiation and the fields of the other dipoles. For uniform material the phases of the stimulated dipoles cancel each other in all the directions and sum up to zero except in the forward direction. Therefore, there is no scattered light in any direction except the forward direction, where the observed effect is refraction.

For a material with non-uniform density, each phase is summed with a different weight and the sum is not zero, so that scattered light may advance in any direction. Light is scattered from scattering centers and the scattered light intensity is equal to the sum of the light intensities of the centers.

A scattering center is a uniform sub-volume of a non-uniform volume. The scattering properties depend on the size of the center volume. For volume size smaller than the stimulating wavelength there will be scattering in all directions, Rayleigh scattering, and for volume size bigger than the wavelength, the scattering will be of small angle, Mie scattering.

Figure-2 shows an observing camera on a satellite looking at a full earth, while the sun is behind its back.

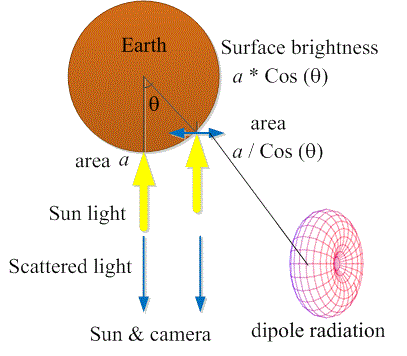
Sunlight brightness a * Cos(θ) on the earth illuminates the area a / Cos(θ) through a. The sun light polarizes the earth surface perpendicular to the light direction. The earth dipoles scatter maximum light back to the sun, and back to an observing camera on a satellite.