van't Hoff's Evidence
Abstract
van't Hoff's theory of the osmotic pressure, for which he received the first Noble prize in chemistry, was
not generally accepted in the years that followed and was replaced by an analysis in terms of chemical potentials.
van't Hoff 's argument, as refined by Rayleigh, and the chemical potential analysis are manifested to be equivalent
Osmosis is the flow of a solvent via a semi-permeable membrane that separates
two volumes of liquid and blocks the passage of solute particles. The solvent flows
from the volume of lower solute concentration to the volume of higher solute concentration.
When solute particles are present only in one volume,
the osmotic pressure is then the pressure on the solution that stops the flow .
van't Hoff derived the formula for the osmotic pressure,
π = c R T,
by analogy with the pressure of an ideal gas of the same concentration and temperature. c is
the molar concentration of solute particles, R is the gas constant, and T is the absolute temperature.
van't Hoff's work was first published in 1887 (1) and he received for it the first Noble prize in
chemistry in 1901, but the arguments in his presentation and his idea of the analogy with the ideal
gas were not generally accepted in the years that followed.
Ten years later, in 1897, Rayleigh who expressed high esteem of van't Hoff's work, but
was aware of shortcomings in his presentation, published a short article that put his arguments
on a firmer ground (2). Rayleigh's presentation was criticized by Kelvin as irrelevant (3), and
shortly after that Gibbs published an analysis of the osmotic pressure in terms of chemical
potentials (4). Since then, chemical potentials serve as an essence to most of the publications and
textbooks that deal with osmosis.
van't Hoff discusses in his article the analogy of solute particles with an ideal gas.
He considers a gas dissolved in water, in a scheme of two cylinders, each equipped with
two moving pistons and two semi-permeable membranes, one membrane is permeable to the
solute gas, and one is permeable to water (figure-1).
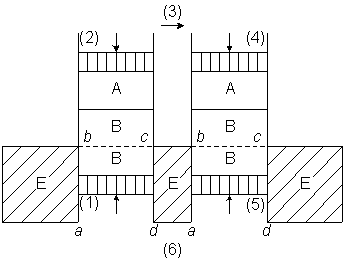
Figure-1: van't Hoff's scheme for discussing osmosis. A is the gas-phase. B is the solution. E is water. The membrane a--b, or c--d, is permeable to water. The membrane b--c is permeable to the gas.
van't Hoff's argument is difficult to follow since he doesn't mention explicitly how the two cylinders are coupled.
Rayleigh considered a cylinder equipped with two moving pistons and two semi-permeable membranes immersed in water that fills the volume between the two membranes. Figure-2, deduced from Rayleigh's article, presents the scheme that he discussed. The upper volume, between the upper piston and a static upper membrane, contains a gas. The upper membrane is permeable to the gas and the gas is partly dissolved in the water between the two membranes. The lower membrane, which also acts as a piston, is permeable to water but blocks the passage of the gas.
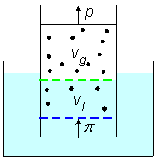
Figure-2: A cylinder equipped with two moving pistons and two
semi-permeable membranes. An upper static membrane is permeable to the
solute gas and a lower membrane is permeable to water and serves also as a
moving-piston.
van't Hoff and Rayleigh constructed a reversible and isothermal closed cycle that includes
stages of solute compression and gas expansion or vice versa. The work done in such a
closed cycle is zero as stated by the second law of thermodynamics postulated by Kelvin.
By applying the law they calculated the osmotic pressure to be equal to the pressure of an
ideal gas of a density that is equal to the solute concentration.
Gibbs analyzed the same system discussed by Rayleigh, as presented in figure-2. He considered
the chemical potentials of water and the gas, and compared each of them in the upper gas volume,
in the middle solution volume, and in the lower water volume. Inputting the chemical potential
of the ideal gas into the calculation, he obtained, not surprisingly, an ideal gas equation
for the osmotic pressure.
In Fermi's book on thermodynamics (5), as well as in other textbooks, the entropy or the free energy
of the ideal gas is used as an input to the calculation. Fermi argues that the free energy of the gas molecules in
the gas phase is equal to their free energy in the solution. Fermi's justification for this argument can be
transformed into considering a reversible closed cycle of a system between two temperatures. Since the entropy change
during the closed cycle is zero, the entropy of solute compression in a low temperature liquid state
will be equal in magnitude to the entropy of solute expansion in a high temperature gaseous state.
Consider the system in figure-2 where Vs is the solution's volume and
cs is the solute-gas concentration in the liquid volume between the two membranes.
Vg is the gas volume and cg is the gas-density
between the upper piston and the upper membrane.
The lower piston moves a small distance up and pushes back a
volume dVs of water out of the solution.
As a result cs dVs solute-gas
molecules leave the solution toward the gas. The upper piston also moves up and
increases the gas-volume by dVg in order to keep the gas-pressure p constant. Therefore:
cg dVg = cs dVs
(1)
G(T, p, Ni) = U + p V - T S
is the Gibbs free
energy of the system where U is the internal energy and S is the entropy.
G is linearly approximated by the sum of the free energies of the system's
components (5-8). Considering the system as the volume between the two membranes,
the condition of reversibility, for constant temperature and pressure, is given by:
ΔG =
Σi(∂G
/ ∂Ni) dNi = 0
(2)
∂G / ∂Ni is the energy required to add or
to remove the i component from the system.
Here there are two components, water and the solute gas.
The work done by the lower piston in order to remove water from the system is
π dVs, where π is the osmotic-pressure. The work done on the
upper piston by the gas molecules that leave the solution is p
dVg, where p is the gas-pressure. Therefore, according to the
reversibility condition (2):
p dVg = π dVs
(3)
And, by equation-(1):
p (cs / cg ) dVs =
Δpi dVs
(4)
So that p (cs / cg ) =
π. The gas pressure, linearly approximated by the ideal gas law, is p =
cg R T, therefore, the osmotic-pressure is:
π = cs R T
(5)
That is, the osmotic-pressure π is
equal to the pressure of a gas of the same density as the solute
concentration.
This discussion, in terms of the free-energy, that follows van't Hoff and Rayleigh,
is essentially equivalent to presentations in textbooks in terms of chemical potentials (5-8).
One mole of the solute gas occupies a volume
Vs = R T / π of the solution. This volume contains
Nw = Vs DH2O / MH2O moles of water.
DH2O is the density of water and MH2O is its molecular weight.
The reversibility condition, equation-(2), becomes:
μsolute + Nw μH2O = 0
(6)
where μi are the chemical potentials.
The volume change involved in removing one mole
of the dissolved gas, by pushing up the lower membrane, is
ΔVs = RT / π,
by van't Hoff formula. Therefore, the chemical potential of the dissolved gas,
which is equal to the work of removing one mole of it, is:
μsolute =
π ΔVs = R T .
The chemical potential of water in the solution, determined from equation (6), is
μH2O =
-π MH2O / DH2O .
van't Hoff's and Rayleigh's original ideas of osmosis were forgotten during the years that passed and abandoned in
favor of supposedly more general and rigorous theories in terms of free energy and chemical potentials.
However, these theories are just another equivalent way of discussing the subject of osmosis, and they
have no advantage of generality and rigor.
See: Thermodynamics and mechanism of osmosis,
Osmosis and Thermodynamics.
References:
- J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen",
Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888)
J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899) - Lord Rayleigh, "The theory of solutions", Nature, vol 55, pp. 253-254 (1897)
- Lord Kelvin, "On Osmotic Pressure against an Ideal Semi-Permeable Membrane", Nature, vol 55, pp. 272-273 (1897)
- J.W. Gibbs, "Semi-Permeable Films and Osmotic Pressure", Nature, vol 55, pp. 461-462 (1897)
- E. Fermi, "Thermodynamics", Dover Publications, Inc., New York , pp. 113-123 (1956)
- W. Pauli, "Thermodynamics and the Kinetic Theory of Gases", Dover Publications, Inc., New York , pp. 73-82 (2000)
- G.H. Wannier, "Statistical Physics ", Dover Publications, Inc., New York , pp. 366-376 (1966)
- K. Huang, "Statistical Mechanics ", 2nd Ed., Wiley, Inc., New York , pp. 43-48 (1977)
On the net: October, 2007.
Danish translation: van't Hoffs Beviser
By the author:
- "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
- "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
- "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
- "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
- "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
- "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
- "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
- "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
- "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
- "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
- "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
- "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
- "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
- "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
- "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).
Links:
- Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
- Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
- My Spin on Lunacy http://www.optics.arizona.edu/Palmer/moon/lunacy.htm
- Five Weeks in a Balloon
- The first man I saw
- "Faster, Faster!"
- Perfection can't be rushed
- The man higher up
- Brains
- The First-Class Passenger
- other