Expansion of an Ideal Gas
Uri Lachish, guma science
![]()
Contents:
Introduction
Elastic Collisions
The gas pressure
Drag
Expansion
Isothermal expansion
Adiabatic expansion
Expansion of a quantum well
1. Introduction
Gas particles in a box collide with its walls and transfer momentum to them during each collision. The gas pressure is
equal to the momentum delivered to a unit area of a wall, during a unit time. Ideal gas particles do not collide with each other but
only with the walls. A single particle moves arbitrarily along some direction until it strikes a wall. It then bounces back, changes
direction and speed and moves towards another wall. The gas expansion equations are derived directly from the law of conservation
of linear momentum and the law of conservation of energy.
2. Elastic collisions
Consider the elastic collision between two particles of mass m and M, moving
toward each other along a straight line as shown in figure-1.
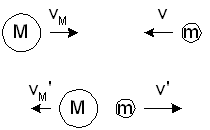
Figure-1: Elastic collision between two particles of mass m and M, moving toward each other along a straight line.
The velocities of the particles before the collisions are v and
vM, and after the collision they are v' and
vM'.
The law of conservation of linear momentum states that:
m v + M vM = m v' + M vM' (1)
and the law of conservation of energy states that:
m v2+ M vM2 = m v'2 + M vM'2 (2)
Division of equation (2) by equation (1) yields:
v - vM = -(v' - vM') (3)
That is, the relative velocity between the particles is conserved during the collision, and the direction is
reversed.
Rearrangement of equations (1) - (2) gives:
(1 + m/M) vM' - (1 - m/M) vM = (m/M) 2v
(4)(1 + m/M) v' + (1 - m/M) v = 2vM (5)
Assume that m is a microscopic particle and M is a macroscopic body. In the limit (m/M) --> 0:
vM' = vM
(6)v' = -(v - 2vM)
(7)The direction of the microscopic particle is reversed and its velocity changes by 2vM, two times the velocity of the macroscopic body. The velocity of the macroscopic body is almost not affected by the collision.
If the velocity of the macroscopic body is extremely slower than that of the microscopic particle, vM << v, then the kinetic energy, ΔEk, transferred from body to body will be, by equations (6) - (7):
Δ
Ek = (m/2) (v'2 - v2) = 2m vM (v + vM) (8)2m vM v, the dominant term on the righthand side of equation (8), is a reversible energy transfer between the microscopic and macroscopic bodies. This energy is proportional to the velocity of the macroscopic body and is independent of its mass. In a front collision, when the two bodies move toward each other, the energy will transfer from the macroscopic to the microscopic body, and in a back collision, when they move at the same direction, the microscopic body will transfer energy to the macroscopic body. The other term, 2m vM2, is an irreversible transformation of kinetic energy into heat, for both cases.
3. The gas pressure
A particle moves with a velocity
v
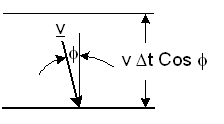
Figure-2: Elastic collision of a particle with a wall.
It will collide with the wall during a time Δt, if its distance from the wall is less than |v| Cosφ Δt. The number ΔNcol of particle collisions with a unit area of the wall during Δt is:
Δ
Ncol = [n ∫f(v) |v| Cosφ d3v] Δt (9)n is the particle density, f(v) is the probability that the particle velocity is v, normalized by ∫4π v2 f(v) dv = 1, and d3v = 2π v2 dv Sinφ dφ . Substituting in equation (9):
ΔNcol = n (∫2π v2 f(v) v dv) (∫Cosφ Sinφ dφ) Δt (10)
The three-dimensional average velocity of particles is <v> =∫4π v2 f(v) v dv. <v> is not zero since the integration is only over positive values. The trigonometric integral over half the sphere is ∫Cosφ Sinφ dφ = 1, ( 0 < φ < π/2), therefore:
ΔNcol = n (<v>/2) Δt (11)
Upon a collision with the wall the particle will transfer a momentum 2mv Cosφ to the wall. The overall momentum ΔM, delivered to a unit area of the wall during Δt, is the sum of momenta delivered by all the colliding particles that come from all directions of the half sphere. Similarly to equations (9) - (10):
ΔM = n 2m (∫2π v2 f(v) v2 dv) (∫Cos2φ Sinφ dφ) Δt (12)
The three-dimensional average is
<v2> =∫4π
v2 f(v) v2 dv,
∫Cos2φ
Sinφ dφ = 1/3, and the pressure
p =ΔM /
Δt is therefore:
p = n m <v2>/3 (13)
The thermal average is calculated by applying Maxwell-Boltzmann distribution:
f(v) = (m / 2πkT)3 / 2 exp(-mv2 / 2kT) (14)
to the calculation of <v> and <v2> (see appendix):
<v> = 4π ∫f(v) v3dv = 2 (2kT / πm)1/2 (15)
<v2> = 4π ∫f(v) v4 dv = 3kT / m (16)
Substituting <v2> in equation (13) yields the pressure:
p = n kT (17)
Equation (17) is the state equation of an ideal gas.
4. Drag within an ideal gas
a. Drag of a perpendicular disc
Consider a flat horizontal disc, of unit area, moving upward at a velocity vM within a
box of an ideal gas.Gas particles that collide with the disc's front surface will leave it with a higher velocity
and particles that collide with the disc's back surface will leave it with a lower velocity.
A particle moves with a velocity vin
toward a moving disc at a velocity vM (figure-3 ).
The particle's velocity is first transformed from a static reference to coordinates that move together with the disc (a).
Then the particle is mirror reflected by an angle
φ in the moving coordinates (b).
Finally, the particle's velocity is transformed back to the static reference (c).
If the disc moves upward, an amount of 2vM will be added to
the vertical component of the reflected velocity, according to equation (7).
The vectorial change of a particle's velocity, will be
vout = -(vin - 2vM),
as is also seen by mirror imaging figure-3a on figure 3c.
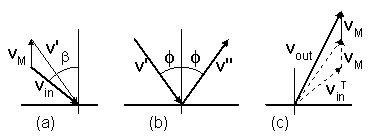
Figure-3: Collision of a particle with a moving disc:
(a) Velocity transformation of a particle from a static reference to coordinates that move
together with the disc.
(b) Mirror reflection of the particle's velocity in the moving coordinates.
(c) Back transformation to the static reference.
Particles above the disc will collide with it if their distance from the disc is less than (|v| Cosφ + vM) Δt, as shown in figure-(4), since the disc moves toward them. Particles below the disc will collide with it if their distance from the disc is less than: (|v| Cosφ - vM) Δt.
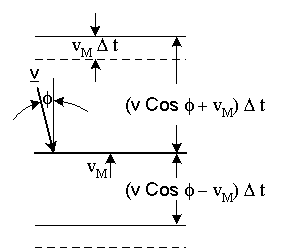
Figure-4: Elastic collision of a particles with a moving disc.
The disc transfers a momentum
m (|v| Cosφ + 2 vM)
, equation (7), to a particle that collides with it from above, and a momentum
m (|v| Cosφ - 2 vM)
to a particle that collides with it from below. So that the net momentum transferred
to two such particles is zero. However, there are more collisions with particles above the disc than below it.
Therefore, a net pressure is formed, oppsing the disc movement.
ΔM1 =
[n m ∫(|v| Cosφ + 2vM) f(v)(|v| Cosφ + vM)
d3v] Δt
The momentum trasferred above the disc is:
and below it is:
ΔM2 =
[n m ∫(|v| Cosφ - 2vM) f(v)(|v| Cosφ - vM)
d3v] Δt
ΔM = [6 n m ∫v Cosφ f(v) vM d3v] Δt
(20)Inserting d3v = 2π v2 dv Sinφ dφ in equation (20) yields:
ΔM = 12 π m n vM (∫ v3f(v) dv) (∫Cosφ Sinφ dφ) Δt (21)
Using 4π ∫ v3f(v)dv = 2 (2kT/πm)1/2 and ∫Cosφ Sinφ dφ = 1, ( 0 < φ < π/2), similarly to equations (10), (15), the net pressure will be:
pex = ΔM / Δt = 6n vM (2kmT/π)1/2
(22)Defining the drag coefficient γ by pex = γ vM, its value will be:
γ = 6n (2mkT/π)1/2 (23)
b. Drag of a tilted disc
A particle with a velocity vin moves at an angle
β toward a tilted moving disc.
The disc's velocity is vM
(figure-5 ). The tilt angle is α.
The particle's velocity is first transformed from a static reference to coordinates that move together with the disc (a).
Then the particle is mirror reflected in the moving coordinates (b).
Finally, the particle's velocity is transformed back to the static reference (c).
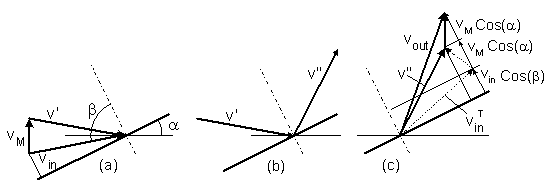
Figure-5: Collision of a particle with a tilted moving disc:
(a) Velocity transformation of a particle from a static reference to coordinates that move
together with the disc.
(b) Mirror reflection of the particle's velocity in the moving coordinates.
(c) Back transformation to the static reference.
and by pex = γ vM, the drag coefficient is:
γ = 6n (2mkT/π)1/2 Cos2(α) (29)
c. Drag of a sphere
The sphere's drag is calculated by dividing the upper half of its surface into elements and applying
equation (28)-(29) to each of them. Figure-5 defines the sphere parameters and coordinates
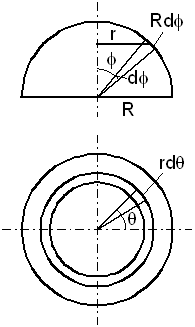
Figure-6: The sphere parameters and coordinates. The upper figure is a front look and the lower figure is a look from above. The sphere moves upward.
R is the sphere radius, φ is the elevation angle observed
in the front look, and θ is the rotation angle observed from
above, and r = R sin(φ).
By (28) the contribution of a surface element
r dθ R dφ to the drag F is
(r = R Sin(φ)):
dF = pex r dπ
R Cos2(φ) dφ
= 6n (2mkT/π)1/2 vM
dθ R2 Sin(φ)
Cos2(φ)
dφ
(30)
The integration over the azimuth angle θ is 2π,
and the integration over the elevation angle φ, between 0
and π/2 is 1/3. Therefore, the drag force is:
F = pex A = γ vM A = 4n (2mkT/π)1/2 vM (πR2) (31)
where A = πR2 is the sphere cross section.
The drag coefficient is:
γ = 4n (2mkT/π)1/2 (32)
5. Expansion
When a wall of the box is a partition that moves at a velocity vM, every particle that collides
with the partition will transfer to it the energy 2m v Cosθ
vM (equation (8)). The overall energy ΔE
, transferred to a unit area of the moving partition, during a time
Δt, is the sum of the energies
delivered by all the colliding particles coming from all directions. The energy is calculated similarly to equation (12):
ΔE = vM n 2m (∫4π v2 f(v) v2 dv) (∫Cos2θ Sinθ dθ) Δt (33)
By using equation (12):
ΔE = p vM Δt = p ΔV (34)
V
Δt is the distance traveled by the partition and it is also the change of the volume ΔV of the box per unit area of the moving partition.The calculation demonstrates that elastic particle collisions with a moving partition is the transformation mechanism of microscopic thermal energy of the particles into macroscopic mechanical work of the partition.
6. Isothermal expansion
The state equation (17), p = (N/V) kT, is inserted into the energy expression (34):
Δ
E = N kT (ΔV/V) (35)n = N/V
, V is the box volume and N is the number of particles in it. The energy is integrated in an isothermal system:∫dE = N kT ∫dV/V (36)
7. Adiabatic expansion of a mono-atomic gas
In an adiabatic system the particles do not exchange energy with the walls by inelastic collisions and the only energy transfer
mechanism is via elastic collisions with a moving partition.
A single particle collides ΔNcol / N = (v/2) Δt / V times, equation (11), with the partition during Δt. During each collision the particle loses (or gains) a velocity 2vM, equation (7), twice the partition velocity in the direction of its movement. A partition that moves in the x-direction will change the vx component of the particle velocity. However, the velocity change will eventually spread to the vy and vz components. Therefore, the change of a particle velocity during Δt will be:
dv = -(1/3) 2vM (v/2) Δt / V = -(v/3) dV/V (37)
since vMΔt = dV. The equation of adiabatic expansion of a mono-atomic gas, without internal degrees of freedom of gas particles, is calculated by integration of equation (37):
v/v0 = (V0/V)1/3
(38)and by equation (13):
p/p0 = (V0/V)5/3
or, by the state equation (17), p = n kT:
T/T0 = (V0/V)2/3 or p/p0 = (T/T0)5/2 (39)
Since:
d(T/T0) = (-2/3) (V/V0)-5/3 d(V/V0))
(40)the work of adiabatic compression or expansion of the gas will be:
W = 0∫V pdV = p0V0 0∫V(V/V0)-(5/3) d(V/V0)
= (3/2) p0V0 0∫T d(T/T0)
= (3/2) (p0V0/T0) (T - T0) = (3/2) N k (T - T0)
8. Expansion of a quantum well
The ground state of a particle within an infinite square well potential that extends from x = 0 to
x = L can be described as a combination of two travelling waves in opposite directions:
ψ
(x, t) = (i/2L) (e-i(kx + wt) - e+i(kx - wt)) (42)where k = π/L and w = hπ2 / 2mL2 . If the boundary at L is moving slowly with a velocity vM , then the waves reflected from it will be Doppler shifted:
k' = k (1 - 2vM/c)
(43)where c = w/k is the velocity of the waves. During a time Δt each wave is reflected c Δt / 2L times by the moving boundary, so the overall shift of the wave number will be:
Δ
k = - k vM Δt / L = - π ΔL/L2 (44)When the well expands from L1 to L2 the wave number will shift, by integration of equation (42), from π/L1 to π/L2. Therefore, the ground state wave function related to L1 will be shifted to the ground state function related to L2.
See:
Boltzmann Transport Equation
Osmosis and Thermodynamics
van't Hoff's Evidence
Appendix: integrals
0∫ ∞xn exp(-a2x2) dx = Γ((n+1)/2) / 2an+1
Γ is the gamma function:
Γ(n) = (n – 1)!
Γ(x + 1) = x Γ(x)
Γ(x) Γ(x + 1/2) = Γ(2 x) π1/2 / 22 x - 1
Γ(1/2) = π1/2
Γ(3/2) = (1/2) π1/2
Γ(5/2) = (3/4) π1/2
References
F.W. Sears, G.L. Salinger, Thermodynamics, Kinetic Theory, and Statistical Thermodynamics (Addison-Wesley, 3rd ed 1975)
pp 254-266, 354-360.
U. Lachish, J. Chemical Education, vol 55(6), 369-371 (1978)
On the net: December 2002, section on drag added July 2006, drag of a sphere added June 2008.
By the author:
- "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
- "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
- "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
- "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
- "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
- "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
- "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
- "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
- "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
- "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
- "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
- "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
- "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
- "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
- "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).
Links:
- Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
- Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
- The Blind Men and the Elephant
- My Spin on Lunacy
- Five Weeks in a Balloon
- The first man I saw
- "Faster, Faster!"
- Perfection can't be rushed
- The man higher up
- Brains
- The First-Class Passenger
- other