New:
New: Osmosis Desalination and Carnot
New
Blue Marble the Uniform Earth Image
The Sun and the Moon a Riddle in the Sky
Osmosis and Thermodynamics
Abstract
van't Hoff formula of osmotic pressure, which is identical to the formula of ideal gas
pressure, is a direct outcome of the second law of thermodynamics. The formula is
derived by applying a closed cycle reversible and isothermal process that follows an
argument in Fermi's book: "Thermodynamics".
Osmosis is the flow of a liquid via a semi-permeable membrane that
blocks the passage of particles dissolved within it. The flow direction
and rate is controlled by pressure on the liquid solution. For a system where the particles
are on a single side of the membrane, the osmotic pressure π,
the pressure that stops the flow, is given by van't Hoff's formula (1):
where c is the molar solute concentration, R is the gas constant, and T is the absolute temperature. van't Hoff derived this formula by analogy with the pressure of an ideal gas of the same concentration and temperature. For this hypothesis he received the first Noble prize in chemistry in 1901, but his idea of the analogy was not generally accepted in the years to come. Regarding osmosis, people usually refer to the general theory of thermodynamics and the identity of van't Hoff's formula of osmotic pressure, to the ideal gas pressure, is considered sometimes as surprising or as a coincidence. People also propose models and mechanisms of solvent pumping by the membrane to account for osmosis. A recent one appears in ref-(2).
Here is a thermodynamic discussion of osmosis that follows Fermi's book "Thermodynamics" (3). Fermi's argument is quoted in Appendix-1.
Consider a vertical cylinder, equipped with an upper and a lower moving piston, divided by a semi-permeable membrane as shown in Figure-1. The cylinder contains a fluid, either a liquid or a gas, or both, that is free to cross the membrane. In addition, there are dissolved particles blocked by the membrane and confined to the cylinder lower volume. It is assumed that there is no chemical interaction between the dissolved particles and the fluid.
Figure-1 describes a cyclic four step reversible process that operates at a constant temperature.

Figure-1: Cyclic isothermal compression and expansion of particles
within a fluid. The fluid is free to
cross the semi-permeable membrane.
(a)- (b): Compression of the particles
within a liquid (blue). The fluid volume is constant.
(b)- (c): Expansion of the fluid to
evaporate all the liquid.
(c)- (d): Expansion of the confined particles within a gas (grey).
The fluid volume is constant.
(d)- (a): Compression of the fluid to partially condense the
gas.
The work of fluid
expansion (b) is equal to the work of fluid compression (d). Therefore, by
the
second law of
thermodynamics, the work of particle compression within the liquid must be
equal to the work of
particle expansion within the gas.
In step-1 the confined
particles in the lower volume are dissolved in a liquid fluid. The two
pistons move up together without changing the fluid volume;
therefore, there is no work involved with the fluid. However, the lower
piston compresses the dissolved particles, between it and the membrane, and does an amount of
work π dV where π is the osmotic
pressure. V is the volume of the dissolved particles and dV is a small
volume change.
In step-2 the upper piston moves up and induces
liquid evaporation of the fluid until it is transformed into a gas. It is assumed
that the dissolved particles are now also in a gas phase.
In step-3 the two pistons move down together, again without changing the fluid volume. The confined
particles push the lower piston, expand and do a work p dV where p is the
gas pressure and dV is the same volume change as in step-1.
In
step-4 the upper piston moves down, compresses the fluid and induces fluid
condensation into a liquid until it arrives at the initial state of the
completed cycle.
Since the process is reversible and isothermal the
overall work done during the closed cycle must be zero. Otherwise it will
violate the second law of thermodynamics as postulated by Kelvin (Fermi,
"Thermodynamics", page 30):
"A transformation whose only final
result is to transform into work heat extracted from a source which is at
the same temperature throughout is impossible."
The work done in step-2, of fluid expansion, is equal to the work done in step-4,
of fluid compression, since the two processes are done between the same
fluid states. Therefore, the compression work, in step-1, of the confined
particles dissolved within a liquid, must be equal to the expansion work,
in step-3, of the confined particles in a gas phase. That is,
π dV = p dV. Therefore, the osmotic pressure of the
particles dissolved within the liquid is equal to the ideal gas pressure
in the gas phase.
The identity of van't Hoff's formula of the osmotic pressure to the formula of the ideal gas pressure is, therefore, a direct and fundamental consequence of the second law of thermodynamics.
The argument leading to the equation depends on the assumption that the solute-solvent interaction does not depend on the solute concentration. States (a) and (b) in Figure-1 have different volumes of solvent interacting with the solute so that in non-ideal solutions they are not the same fluid states. As a result the work in step 2 will not be equal to the work in step 4 and the equation will be only approximate.
Osmosis is discussed in textbooks in terms of the free energy G. ΔG = 0, or in terms of the entropy S,
ΔS = 0, both for a reversible process. For a reversible closed-cycle and isothermal process:
where ΔQ is the heat transferred to the heat bath, and ΔW is the work done by the system, both in a closed cycle.
Therefore discussions in terms of G, S, or W of a reversible isothermal process are fully equivalent. The discussion of osmosis in terms of W, as presented here, is equivalent to a discussion in terms of the free energy G.
In Fermi's discussion of osmosis, in terms of the free energy, he applies the entropy of free particles (Fermi, "Thermodynamics", p. 115, equation (153)) which he justifies by considering the system in a vaporized thermodynamic state (see Appendix-1. The idea is followed here). The whole matter is ideal gas in - ideal gas out, so that van't Hoff formula is hardly surprising.
When static pressure is built up within a fluid, Pascal law postulates that the pressure will be distributed equally within the fluid volume and will be perpendicular to the surface of the fluid boundary (gravitation not included). The law is a direct consequence of the conservation law of linear momentum.
Since the dissolved particles are prevented from leaving a volume by a semipermeable membrane they will exert pressure on it (a loose quotation of Einstein (4), see Appendix-2).
Fermi expresses the same idea ("Thermodynamics", page 122, see Appendix-1):
"... Then the pressure on the side
of the membrane facing the solution will be increased by the
impacts against it of the molecules of the dissolved sub-
stances, which cannot pass through the membrane..."
A solute particle exerts pressure by delivering momentum to the membrane. It delivers momentum also to its neighbor molecules, so that the time averaged momentum delivered to the membrane and to the neighbors in all directions is zero, as required by conservation of linear momentum. The non zero momentum delivered to the neighbors, not including the membrane, spreads in all directions toward the solution boundaries and generates pressure on them.
Whenever an osmotic pressure is built-up, according to Pascal law it will act equally on all of the solution boundaries. It will then push any boundary that is free to move. The osmotic pressure acts on a moving boundary from inside the solution, and in order to keep the system under balance a similar extra external pressure should act on it from outside. If the external pressure is reduced below the osmotic pressure, then solvent will flow via the membrane into the solution, and if the external pressure is increased above the osmotic pressure, then the solvent will flow out of the solution.
These conclusions are direct consequences of fundamental laws. The role of the membrane in osmosis is just to let the solvent go through it and to block the solute. There is no need of microscopic solvent pumping by the membrane.
van't Hoff, in his paper (1), presents a flow scheme in order to verify the osmotic pressure formula. The scheme is not clear and difficult to follow. However, it does consist of a closed cycle that includes an expansion work of particles in a gas phase and a compression work in solution, or vice versa.
van't Hoff also discusses the mechanism of osmosis:
"The mechanism by which, according to our present conceptions, the elastic pressure of gases is produced is essentially the same as that which gives rise to osmotic pressure in solutions. It depends, in the first case, upon the impact of the gas molecules against the wall of the vessel; in the latter, upon the impact of the molecules of the dissolved substance against the semipermeable membrance, since the molecules of the solvent, being present upon both sides of the membrane through which they pass, do not enter into consideration."
van't Hoff original paper on osmosis thus presents a thermodynamic derivation of the osmotic pressure formula and also a rigorous mechanism of osmosis as evidenced by considering Pascal law. A high esteem of van't Hoff work was expressed by Lord Rayleigh (5) (see appendix-3):
"If I suggest a somewhat modified
treatment, it is not that I see any unsoundness in van't
Hoff's argument, but because of the importance of
regarding a matter of this kind from various points of
view."
When either solvent molecules or dissolved particles, at liquid boundaries other than the membrane, are prevented from leaving the liquid, they will exert pressure on the boundaries (this remark again follows Einstein (4), see Appendix-2). Therefore, by Neuton's third law, the boundaries exert back the same pressure on the liquid. This pressure, that comes from the molecular attraction forces at the liquid surface, is by far higher than the membrane generated osmotic pressure which is only a small disturbance to it. Therefore the pressure on the liquid is always positive. Contrary to the semi-permeable membrane, at the other boundaries of the pure solvent, or of the solution, there is no difference between solvent and solute collisions with them,
See: The equivalence of van't Hoff's and Rayleigh's arguments with the analysis of chemical potentials.
van't Hoff's Evidence
Appendix-1: THERMODYNAMICS by ENRICO FERMI
Prentic-Hall 1937. Dover Publications, Inc. New York, NY 1956
Chapter VII: The Thermodynamics of Dilute
solutions
Page 115:
... "If we now integrate (150), we obtain
the expression for
the entropy:
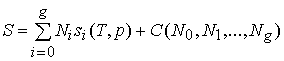 .
(152)
.
(152)
The constant of integration C, which is constant
only with
respect to T and p, depends on the N's;
we have put this in
evidence in (152). We can determine the value of
this
constant as follows:
Since no restriction has been placed on
the manner in
which T and p may vary, the expression (152) for S still
applies if we choose p so small and T so large
that the entire
solution, including all
solutes, vaporizes. Our system
will then be completely gaseous, and for
such a system we
already know that the entropy is equal to the sum of
the
partial entropies of the component gases (see section 23).
But the entropy of one mole of a gas at the partial pressure
pi and having the molecular
heat Cpi is (see equation (87)):
![]() .
(153)
.
(153)
Hence, for our mixture of gases we have (since the partial
pressure pi of the substance Ai is
equal to
pNi /
(N0 + +
Ng), where p is the total pressure):
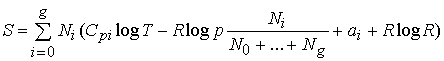
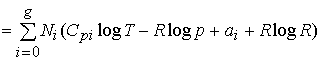
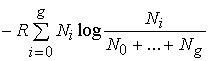 .
.
If we compare this with (152), which applies to our
gaseous mixture also, we find that:
![]() ,
,
and
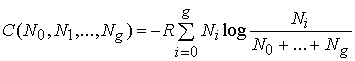 .
(154)
.
(154)
But the constant
C(N0,
N1, ,
Ng)
does not depend on
T or p. Its value (154)
therefore applies not only to the
gaseous mixture, but also to the
original solution. Hence,
(152) becomes:
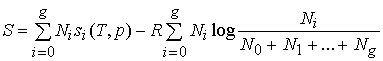 . (155)"
. (155)"
Page 122:
"The osmotic pressure of a dilute solution is equal to the
pressure exerted by an ideal gas at the same temperature and
occupying the same volume as the solution and containing a
number of moles equal to the number of moles of the solutes
dissolved in the solution.
This simple thermodynamical result can be easily inter-
preted from the point of view of the kinetic theory. We
consider a container divided into two parts by a semi-
permeable membrane with pure solvent in each part.
Since the solvent can pass freely through the semipermeable
membrane, the pressure on both sides of the membrane will
be the same. Now let us dissolve some substances in one
part and not in the other. Then the pressure on the side
of the membrane facing the solution will be increased by the
impacts against it of the molecules of the dissolved sub-
stances, which cannot pass through the membrane and
which move about with a velocity that depends on T. The
larger the number of molecules dissolved and the higher the
temperature, the larger will be the number of impacts per
unit time and, hence, the greater the osmotic pressure.
It can be shown from the kinetic theory that
the velocities of
molecules of the dissolved substances are not affected by
the molecules' being in solution, but are equal to the velocit-
ies that they would have if they were in a gaseous state.
Therefore, both the number and the intensity of the impacts
of the molecules of the dissolved substances against the
membrane are equal to the number and intensity of the
impacts that one expects for a gas. The pressures exerted
in both cases are therefore equal."
Appendix-2: INVESTIGATIONS ON THE THEORY OF THE
BROWNIAN MOVEMENT by ALBERT EINSTEIN (4),
Methuen and Co., Ltd., 1927, Dover Publications, Inc. New York, NY 1956
Page-3:
..."We must assume that the
suspended particles perform an irregular move-
ment even if a very slow one in the liquid, on
account of the molecular movement of the liquid ;
if they are prevented from leaving the volume V*
by the partition, they will exert a pressure on the
partition just like molecules in solution."
Appendix-3: THEORY OF SOLUTIONS - LORD RAYLEIGH (5)
"As some recent viva voce remarks of mine have received
an interpretation more wide than I intended,
I shall be glad to be allowed to explain that when (now
several years ago) I became acquainted with the work of
van't Hoff I was soon convinced of the great importance
of the advances due to him and his followers. The subject
has been prejudiced by a good deal of careless
phraseology, and this is probably the reason why some
distinguished physicists and chemists have refused their
adhesion. It must be admitted, further, that the arguments
of van't Hoff are often insufficiently set out, and
are accordingly difficult to follow. Perhaps this remark
applies especially to his treatment of the central theorem,
viz. the identification of the osmotic pressure of a dissolved
gas with the pressure which would be exercised
by the gas alone if it occupied the same total volume in
the absence of the solvent. From this follows the formal
extension of Avogadro's law to the osmotic pressure of
dissolved gases, and thence by a natural hypothesis to the
osmotic pressure of other dissolved substances, even
although they may not be capable of existing in the
gaseous condition. If I suggest a somewhat modified
treatment, it is not that I see any unsoundness in van't
Hoff's argument, but because of the importance of
regarding a matter of this kind from various points of
view."
References:
- J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen",
Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
translated by W. Ramsay, Philosophical Magazine, S. 5. Vol 26. No. 159. Aug., pp. 81-105 (1888) J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899) - A. V. Raghunanthan and N. R. Aluru, "Molecular Understanding of Osmosis in Semipermeable Membranes" Physical Review Letters, vol 97, 024501, pp. 1-4 (2006)
- E. Fermi, "Thermodynamics", Dover Publications, Inc., New York, pp. 115-123 (1956)
- A. Einstein, "On
the Motion of Small Particles Suspended in Liquids at Rest
Required by the Molecular-Kinetic Theory of Heat",
Originally published in Annalen der Physik 17 [1905]: 549-560
A. Einstein, "Investigations on the Theory of the Brownian Movement", translated by A.D. Cowper, Dover Publications, Inc., New York, pp. 1-18 (1956) - Lord Rayleigh, "The theory of solutions", Nature, vol 55, pp. 253-254 (1897)
On the net: January, 2007.
By the author:
- "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
- "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
- "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
- "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
- "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
- "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
- "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.pdf, January (2007).
- "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
- "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
- "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
- "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
- "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
- "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
- "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
- "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
- "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).
Links:
- Thermodynamics Research Laboratory, https://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
- Thermodynamik - Warmelehre, https://www.schulphysik.de/thermodyn.html
- The Blind Men and the Elephant
- My Spin on Lunacy
- Five Weeks in a Balloon
- The first man I saw
- "Faster, Faster!"
- Perfection can't be rushed
- The man higher up
- Brains
- The First-Class Passenger
- other