Uri Lachish, guma science

Why the osmotic pressure of a solution is equal to a gas pressure of the same particle concentration?

Summary
The osmotic pressure is a direct consequence of the law of conservation of linear momentum.

Every molecule within a solution, solvent or solute, interacts with its neighbors. The average overall momentum delivered to a molecule by its neighbors is zero, otherwise, the molecule will move and follow the direction of the non-zero momentum, according to Newton's second law. Therefore, according to Newton's third law, the average overall momentum that a molecule delivers to its neighbors is also zero. Non-zero momentum fluctuations do exist, however, and generate the Brownian movement.

A solute molecule located nearby the semi-permeable membrane interacts with the membrane and delivers momentum to it in a some specific direction. Therefore, it must deliver a non-zero momentum to its neighbor molecules in other directions. The overall average momentum, delivered by the molecule to both the membrane and neighbor molecules, must be zero. The momentum delivered to the neighbors transfers further to next neighbor molecules through the solution, finally reaches the solution boundaries, and generates the osmotic pressure.

Gas in a box
Gas particles, contained in a box, collide with its walls and transfer momentum to them during each collision. The gas pressure is equal to the momentum transferred to a unit area of a wall, during a unit time.

In an ideal gas the particles do not collide with each other but only with the walls. A single particle moves arbitrarily along some direction until it strikes a wall, it then changes direction and speed and moves towards another wall. The law of conservation of linear momentum requires that on the average of many collisions the particle transfers similar momentum in all directions.

The average thermal velocity of the particle, and therefore, its linear momentum, increases at higher temperatures.

If one wall of the box is a moving partition, the gas will push it, against an opposing force, by a force equal to the pressure times the partition area (Fig. 1). If the gas force is higher than the opposing force, the box volume will expand. Particles that collide with the moving partition will transform their kinetic thermal energy into macroscopic mechanical work. If the opposing force is higher than the gas force, it will compress the gas and transform the mechanical work of the movement into thermal energy of the particles.

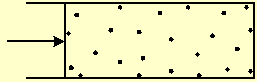
Fig. 1 A gas pushes a partition with a force equal to the pressure times the partition area. The pressure is equal to the momentum transferred to a unit area of a wall, during a unit time.

Liquid
Liquid particles move freely with respect to each other, but the liquid is nearly incompressible. The average distances between the particles, and the liquid volume, are nearly independent of external forces. Particle attraction, that predominates at longer distances, balances particle repulsion that predominates at shorter distances, and the net force between the particles is zero at the equilibrium distance.

The thermal momentum of a particle in a liquid is the same momentum had it been in a gas phase. However, in the liquid it moves only a short distance in one specific direction before it collides with a neighbor particle and changes its direction.

When a boundary of a liquid blocks the instantaneous movement of a particle, the particle will transfer momentum to the boundary and generate pressure on it just like a gas particle. The collisions of particles between themselves, and with the liquid boundary, lead to a small expansion of the liquid volume. The expansion induces a net particle attraction force that balances the pressure on the liquid boundary. There is no external force that holds the liquid together and balances the pressure as in the case of a gas in a box. No work is done by or on external forces.

Is the internal pressure within a liquid real? Well, for example, in a star the gravitational attraction force balances the thermal "liquid" pressure. When the star cools the pressure will drop and the star will shrink or collapse. So, the pressure within a liquid seems very real at least on a cosmological scale.

Fig. 2 illustrates a toy of steel balls, hung on wires along a line, that demonstrates the momentum transfer between liquid particles. A ball at one end is displaced away and let go. The ball hits its neighbor, transfers momentum to it and stops. Each ball along the line transfers in its turn the momentum to its next neighbor, without apparent movement. Upon receiving the momentum, the last ball is displaced from the line by the same distance as that of the first ball.

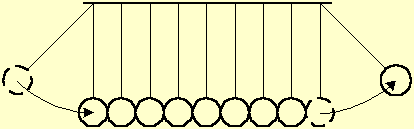
Fig. 2 A displaced ball hits a series of balls hung along a line. Each ball transfers the momentum to its next neighbor, without apparent movement. The last ball is displaced by the same distance as that of the first ball.

A liquid particle that strikes a neighbor particle, transfers momentum to it, and starts a complicated series of further particle collisions in all directions. However, the conservation law of linear momentum requires that the momentum associated with the collisions will advance in the direction the first strike. The collisions spread until they reach liquid boundaries and transfer the momentum to them. On the average of many collisions with its neighbors a liquid particle transfers the same momentum in all directions, just like a gas particle. In both cases the law of conservation of linear momentum requires that the average vectorial sum of momenta, delivered by the particle, is zero.

Solution
Consider a liquid within a box, separated by a semi-permeable membrane into two volumes (Fig. 3), where one volume also contains dissolved particles. The membrane allows the liquid to flow freely through it but blocks the movement of the solute.

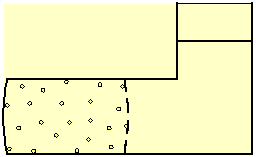
Fig. 3 Dissolved particles, blocked by a semi-permeable membrane, generate osmotic pressure on all the boundaries of the volume that contains them. The pressure curves the surface of a flexible membrane, and of any other flexible boundary of the solution.

When a series of collisions between liquid particles reaches the membrane, it matters which is the last particle closest to it. A liquid particle will transfer the momentum via the membrane into the pure liquid towards the opposing boundary. A solute particle will transfer the momentum to the membrane and generate pressure on it, the osmotic pressure.

A solute particle that has collided with the membrane will bounce back and transfer momentum to a nearby liquid particle. This momentum is further transferred by collisions between liquid particles until it reaches the opposing boundary of the solution and generate pressure on it. In this way solute particles, located near the membrane, generate osmotic pressure on all the boundaries of the solution, and not only on the membrane.

The osmotic pressure on all the solution boundaries is a direct result of the law of conservation of linear momentum. A solute particle, that has delivered momentum to the membrane, must deliver momentum also to the other boundaries in order to balance the overall average momentum to zero.

A series of collisions between liquid particles that starts or ends at the membrane causes the osmotic pressure. Series of collisions that start and end at other boundaries contribute to the internal liquid pressure and do not affect the osmotic pressure.

The average thermal momentum of solute particles is the same in a solution as in a gas phase at the same temperature. It is not a coincidence, therefore, that the osmotic pressure is equal to an ideal gas pressure of the same particle concentration. In this respect the two systems differ only by the mechanism of momentum transfer from wall to wall. A gas particle moves between the walls and "personally" transfers the momentum to them. A solute particle transfers the momentum to the solution boundaries via a series of multiple particle collisions within the liquid.

The osmotic pressure will curve the surface of a somewhat flexible membrane and might even tear it if the membrane is not strong enough. It will also curve any other flexible boundary of the solution.

Citations
"The mechanism by which, according to our present conceptions, the elastic pressure of gases is produced is essentially the same as that which gives rise to osmotic pressure in solutions. It depends, in the first case, upon the impact of the gas molecules against the wall of the vessel; in the latter, upon the impact of the molecules of the dissolved substance against the semipermeable membrane, since the molecules of the solvent, being present upon both sides of the membrane through which they pass, do not enter into consideration."

J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen", Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888)
J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899)

"We must assume that the suspended particles perform an irregular movement - even if a very slow one - in the liquid, on account of the molecular movement of the liquid; if they are prevented from leaving the volume V* by the partition, they will exert a pressure on the partition just like molecules in solution."

A. Einstein, Ann. d. Phys., 17, p. 549, 1905,
"On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat"
"Investigations on the Theory of the Brownian Movement", edited by R. Furth, translated by A.D. Cowper, Dover Publications, Inc., New York (1956) p 3.

"We consider a container divided into two parts by a semipermeable membrane with pure solvent in each part. Since the solvent can pass freely through the semipermeable membrane, the pressure on both sides of the membrane will be the same. Now let us dissolve some substances in one part and not in the other. Then the pressure on the side of the membrane facing the solution will be increased by the impacts against it of the molecules of the dissolved substances, which cannot pass through the membrane and which move about with a velocity that depends on T. The larger the number of molecules dissolved and the higher the temperature, the larger will be the number of impacts per unit time and, hence, the greater the osmotic pressure.
It can be shown from the kinetic theory that the velocities of molecules of the dissolved substances are not affected by the molecules' being in solution, but are equal to the velocities that they would have if they were in a gaseous state. Therefore, both the number and the intensity of the impacts of the molecules of the dissolved substances against the membrane are equal to the number and intensity of the impacts that one expects for a gas. The pressures exerted in both cases are therefore equal."

E. Fermi, "Thermodynamics", Dover Publications, Inc., New York (1956) p 122.

Osmosis, diffusion and reversibility
Fig. 4 shows a vessel divided by a semi permeable membrane into a left side that contains solution, and a right side that contains pure water. A moving partition pushes water through the membrane.

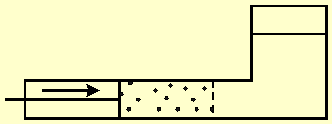
Fig. 4 A vessel divided by a semi permeable membrane into a left side that contains solution, and a right side that contains only pure water. A moving partition pushes water through the membrane.

The partition's external pressure on the solution controls the direction and rate of water flow through the semi permeable membrane. If the external pressure is equal to the osmotic pressure there will be no water flow. If the external pressure is slightly above the osmotic pressure, it will force water to flow from the solution side, through the membrane, into the pure water side. If the external pressure is slightly below the osmotic pressure, it will induce water flow from the pure water side into the solution side. Thus, the external pressure controls the water flow through the membrane. A process, where an external force controls the direction and rate of change of a parameter within a system, is a reversible thermodynamic process.

When solid salt is put into water it will dissolve and the salt particles will diffuse and become equally dispersed in the water volume. External force cannot stop and reverse the movement of the diffusing salt particles. Diffusion is an irreversible thermodynamic process.

Osmosis is a reversible thermodynamic process, therefore, diffusion is not osmosis. Diffusion is irreversible.

Citation
"It has been already mentioned above that a cylinder, provided with semipermeable walls and piston, when immersed in the solvent, allows any desired change in concentration to be produced in the solution beneath the piston by exerting a proper pressure upon the piston, just as a gas is compressed and can then expand; only that, in the first case the solvent, in these changes in volume, moves through the wall of the cylinder. Such processes can, in both cases, preserve the condition of reversibility with the same degree of ease, provided that the pressure of the piston is equal to the counter-pressure, i.e., with solutions, to the osmotic pressure."

J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen", Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888)
J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899)

On the net: December 2001, revised January 2002, summary added June 2003, citations added February 2004.

French translation by Mary Orban: Osmose sur plus

See:
Osmosis Reverse Osmosis and Osmotic Pressure what they are
Osmosis and Thermodynamics
van't Hoff's Evidence

By the author:

1. "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
2. "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
3. "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
4. "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
5. "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
6. "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
7. "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
8. "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
9. "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
10. "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
11. "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
12. "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
13. "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
14. "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
15. "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).

Links:

1. Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
2. Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
3. The Blind Men and the Elephant
4. My Spin on Lunacy
5. Five Weeks in a Balloon
6. The first man I saw
7. "Faster, Faster!"
8. Perfection can't be rushed
9. The man higher up
10. Brains
11. The First-Class Passenger
12. other