Energy of Seawater Desalination

Uri Lachish, guma science

Abstract: Calculation of the minimal energy of seawater desalination achieved in a reversible thermodynamic process.

Thermodynamic principles state that any method of water desalination will be most efficient, if it involves a reversible thermodynamic process. The same energy is invested in any reversible desalination process, and it is independent of the detailed technology employed, exact mechanism, or number of process stages. Calculation of the energy for a particular reversible system is good for all, and it serves as the lower energy limit for any other process.

Osmosis is, in principle, a reversible process, though, its application deviates from reversibility. The energy of seawater desalination by osmosis will be calculated.

Osmosis is the phenomenon of water flow through a semi permeable membrane that blocks the transport of salts through it. The external pressure on the salt solution determines the speed and direction of water flow through the membrane.

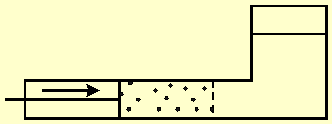
Figure-1 shows a vessel divided by a semi permeable membrane. The left side contains seawater, and a moving partition pushes the water through the membrane. The membrane blocks salt transport and only pure water flows through it. Therefore, the right side of the vessel will contain only pure water. The work W done by the partition is equal to the force F acting on it, multiplied by the distance x that it travels. The process is reversible since the direction of the partition movement, and therefore, also of the water flow through the membrane, can be reversed at any given moment.

The force acting on the partition is equal to the osmotic pressure multiplied by the partition area. The osmotic pressure π is given by van't Hoff formula [1]:

π = cRT

where c is the molar concentration of the salt ions, R = 0.082 (liter∙bar) / (deg∙mol), is the gas constant, and T = 300 K is the ambient temperature on the absolute temperature scale (Kelvin).

The amount of salt in seawater is about 33 gram / liter. Seawater contains a variety of salts, but the calculation will be simplified by assuming that all the salt is sodium chloride (NaCl). The atomic weight of sodium is 23 gram, and of chlorine is 35.5 gram, so the molecular weight of NaCl is 58.5 gram. The number of NaCl moles in seawater is, therefore, 33 / 58.5 = 0.564 mol / liter. (not familiar? see "Chemical measures and units").

When NaCl salt dissolves in water it dissociates into Na⁺ and Cl^- ions. There are two ions per salt molecule, so the ions' concentration is twice the molecules' concentration. c = 2∙0.564 = 1.128 mol / liter. Inserting the values into the van't Hoff formula yields the osmotic pressure:

π = 1.128∙0.082∙300 = 27.8 bar

or, 27.8 kilogram per square centimeter.

Assume now that the partition area is one square centimeter. It then has to travel a distance of 1000 cm, or, 10 meters, in order to push one liter of solution through the membrane. The work of this travel is:

W = F∙x = 27.8∙1∙10 = 278 kg meter / liter

or, 2780 Joules / liter, since 10 Joules are equal to 1 kg∙meter. (Or, 2780 / 3600 = 0.77 (kWatt hour / (cubic meter)). One kilocalorie (kcal) is equal to about 4200 Joules, therefore, the work is 2780 / 4200 = 0.66 kcal / liter.

0.66 kcal / liter is the minimum energy required to desalination of one liter of seawater, regardless of the technology applied to the process.

It is interesting to compare this energy to the heat required to boil one liter of water and condense its vapors. About 70 kcal are required to heat one liter to the boiling temperature, then more 540 kcal are required to boil it. Most of the invested heat comes back during condensation and a lot of it is recoverable by use of heat exchangers. Yet it seems difficult to compete with the energy efficiency of desalination by reverse osmosis.

Producing a volume of desalinated water requires the pumping of a higher volume of seawater. Part of the input seawater is transformed into output desalinated water, and part of it goes back to the sea as a high-salinity water. The ratio of the desalinated water output-volume to the seawater input-volume used to produce it is called the water recovery ratio.

Practical desalination systems are never fully reversible and there are energy losses that are due unavoidable irreversible contributions. These losses, that depend on the water recovery ratio, increase the energy of desalination above the reversible thermodynamic limit.

See details: Optimizing the Efficiency of Reverse Osmosis Seawater Desalination

Note
The work W of desalination is:

W = F∙x = π∙A∙ x = π∙V

Where π is the osmotic pressure, A is the partition's area, and A∙x = V is the volume of pumped water.
In different units:

W = π∙V ∙100

for W in Joules (Watt seconds), π in bars, and V in Liters. Or:

W = π∙V∙(100 / 3600) = π∙V / 36

for W in kWatt hours, π in bars, and V in cubic meters.

References:
J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen", Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888) J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899)

On the net: April 2000.

See:
Osmosis Reverse Osmosis and Osmotic Pressure what they are
Desalination machine

A Pipe of Fresh Water instead of "Canal of the Seas"

By the author:

"Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
"Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
"The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
"Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
"van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
"Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
"Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
"Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
"Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
"Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
"Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
"Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
"Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
"Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
"Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).

Links:

Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
The Blind Men and the Elephant
My Spin on Lunacy
Five Weeks in a Balloon
The first man I saw
"Faster, Faster!"
Perfection can't be rushed
The man higher up
Brains
The First-Class Passenger
other