Osmosis Reverse Osmosis and Osmotic Pressure what they are

π = cRT

where c is the molar concentration of the solute, R = 0.082 (liter∙bar) / (deg∙mol), is the gas constant, and T is the temperature on the absolute temperature scale (Kelvin).

van't Hoff received the first Nobel prize in chemistry, in 1901, for his interpretation of osmosis.

For example, water that contains 33 gram / liter of sodium chloride (NaCl), typical of seawater, has an ionic concentration of c = 1.128 mol / liter. Inserting the values into the van't Hoff formula, for the ambient temperature T = 300 K, yields the osmotic pressure:

π = 1.128 ∙ 0.082 ∙ 300 = 27.8 bar

or, 27.8 kilogram per square centimeter.

The osmotic pressure does not depend on the solute type, or its molecular size, but only on its molar concentration, as the formula states.

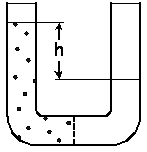
Figure-1 shows connected vessels separated by a semi-permeable membrane. If there is only water in the device, the level will be the same at both arms. When solute molecules are added to one arm, water will start to flow into it, so that its level will go up at this arm, and down at the other arm. The system will stabilize when the osmotic pressure is balanced by the hydrostatic pressure generated by the difference h in the water levels.

where ρ is the water specific gravity. (ρ = gd, where d is the water density and g is the gravity acceleration).

The conservation laws of energy and momentum require that whenever particles collide with a moving wall, they will change direction and increase or decrease their speed. Thus, they transfer both momentum and energy to the wall. Therefore, the process of elastic collisions with a moving wall is the mechanism by which the microscopic kinetic energy of the particles is transformed into macroscopic mechanical work [1].

The conservation law of momentum requires that solute molecules, that generate osmotic pressure on the semi-permeable membrane, must generate, via the volume of the solution, the same osmotic pressure on all the solution boundaries, including its free surface. In this respect the osmotic pressure acts according to Pascal law.

During water flow through the membrane, the osmotic pressure, that operates also on the moving free surface of the solution, will push it upward. Thus the pressure on the free surface is responsible to water pumping from the water arm to the solution arm. This discussion of the flow mechanism usually does not appear in textbooks that deal with osmosis. The effect of the osmotic pressure on the free surface of the solution was first suggested by Hulett in 1902 [5], but received little attention. It seems to have only few proponents since then [6 - 15].

Osmosis is a reversible thermodynamic process. That is, the direction of water flow through the membrane can be reversed at any moment by proper control of the external pressure on the solution. Contrary to that, mixing a teaspoon full of sugar in a cup of tea is an irreversible thermodynamic process of sugar diffusion within water. There is no way to reverse the process at any given moment and un-mix the sugar back to the spoon.

Reversibility is a fundamental idea of thermodynamics. Osmosis is a reversible process, while sugar diffusion in water is not. Diffusion is an irreversible process.

In order to produce drinking water from seawater, by reverse osmosis, the pressure p of the salty water should be increased above the osmotic pressure, so that clean water will cross the semi-permeable membrane and accumulate at its other side. Production of drinking water from a volume V of seawater requires a minimal input of energy E given by:

E = p∙V / 36

for E in kWatt hours, p in bars, and V in cubic meters.

If the pressure p is lower than the osmotic pressure, then clean water will flow back through the membrane toward the salty water. It is possible, by this process, to produce energy from "mixing" clean water with salty water via the membrane.

It is not possible to produce drinking water from seawater, in any process, without energy input. Had it been possible, then clean water would be produced without energy input, then it would be "mixed" back, via a semi-permeable membrane to produce energy, and then the process would be repeated again and again. This is a "perpetuum mobile" that produces net energy from nothing, that is clearly not possible.

The minimum energy required to produce drinking water from salty water is calculated by putting the osmotic pressure π into the formula. For the pressure calculated above the energy is:

E = 27.8 ∙ 1 / 36 = 0.77 (kWatt hour) / (cubic meter) = 0.66 kcal / liter

Compare that to 1 kcal required to raise the water temperature of one liter by one degree Celsius, and to 540 kcal required to boil one liter of water.



What do the greatest people of science think on osmosis?

"We must assume that the suspended particles perform an irregular movement - even if a very slow one - in the liquid, on account of the molecular movement of the liquid; if they are prevented from leaving the volume V* by the partition, they will exert a pressure on the partition just like molecules in solution."
- Albert Einstein [2].

"Then the pressure on the side of the membrane facing the solution will be increased by the impacts against it of the molecules of the dissolved substances,"
- Enrico Fermi [3].

See:
Why the osmotic pressure of a solution is equal to a gas pressure of the same particle concentration?
More on Osmosis
Energy of Seawater Desalination
Osmosis and Thermodynamics
van't Hoff's Evidence

References:

1. F.W. Sears and G.L. Salinger, "Thermodynamics, Kinetic Theory and statistical Thermodynamics", 3rd Ed., 16^th printing, Addison Wesley, Reading Massachusetts (1986) pp. 250-266
2. A. Einstein, "On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat", Originally published in Annalen der Physik 17 [1905]: 549-560
   A. Einstein, "Investigations on the Theory of the Brownian Movement", translated by A.D. Cowper, Dover Publications, Inc., New York, pp. 1-18 (1956)
3. E. Fermi, "Thermodynamics", Dover Publications, Inc., New York (1937) pp. 118-123
4. J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen", Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
   J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
   translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888)
   J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
   in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
   translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899)
5. G.A. Hulett, Acta. Phys. Chem. 42, 353 (1902)
6. K.F. Herzfeld, Phys. Z. 38, 58 (1937)
7. K.J. Mysels and S.C. Copeland, "Introduction to the Science of Chemistry", Ginn and Co., Boston (1952) p. 127
8. K.J. Mysels, "Introduction to Colloid Chemistry", Interscience, New york (1959) Ch. VI
9. P.F. Scholander, Proc. Natl. Acad. Sci. U.S.A., 55, 1407 (1966)
10. P.F. Scholander, Microvasc. Res., 3, 215 (1971)
11. H.T. Hammel and P.F. Scholander, "Osmosis and Tensile Solvent", Springer, New York (1976)
12. H.T. Hammel, Science, 192, 748 (1976)
13. K.J. Mysels, J. Chem. Ed., 55, 21 (1978)
14. U. Lachish, J. Chem. Ed., 55, 369 (1978)
15. K.J. Mysels, J. Phys. Chem. B, 101, 1893 (1997), and references therein.

On the net: February, revised, October, 1998. References added, October, 1999.

Scattering of Directional Light
Scattering of Directional Light

By the author:

1. "Thermoelectric Effects Peltier Seebeck and Thomson",
   Abstract: https://urila.tripod.com/Thermoelectric_abstract.htm
   Full page: https://urila.tripod.com/Thermoelectric.pdf, February 2014.
   
   https://www.researchgate.net/publication/301647437_Thermoelectric_Effect_Peltier_Seebeck_and_Thomson
   
   
2. "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
   
   https://www.researchgate.net/publication/301853213_Osmosis_Desalination_and_Carnot
   
   
3. "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
   
   https://www.researchgate.net/publication/318056635_Light_Scattering
   
   
4. "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/Moon.pdf, July (2011).
   
   
5. "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
6. "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
7. "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
8. "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
9. "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
   
   https://www.researchgate.net/publication/310458654_Optimizing_the_Efficiency_of_Reverse_Osmosis_Seawater_Desalination
   
   
10. "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
    
    https://www.researchgate.net/publication/303537166_Boltzmann_Transport_Equation
    
    
11. "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
12. "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
13. "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
14. "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
    
    https://www.researchgate.net/publication/310458597_Osmosis_Reverse_Osmosis_and_Osmotic_Pressure
    
    
15. "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
16. "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).

Links:

1. Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
2. Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
3. The Blind Men and the Elephant
4. My Spin on Lunacy
5. Five Weeks in a Balloon
6. The first man I saw
7. "Faster, Faster!"
8. Perfection can't be rushed
9. The man higher up
10. Brains
11. The First-Class Passenger
12. Zumba