אוסמוזה התפלה וקרנו

תמונה-1: סרט גומי במצב מתוח – דוגמה לתהליך הפיך. הוספה לכוח המתיחה מאריכה את הסרט. הפחתת הכוח לערכו הקודם מחזירה את הסרט לאורכו הקודם.


        לא כל התהליכים הפיכים. למשל, ערבוב כפית מלאה בסוכר בכוס תה. לא ניתן להוציא בחזרה את הסוכר על-ידי הפיכת תנועת הכפית לאחור. ערבוב סוכר בכוס תה הוא תהליך בלתי הפיך.

        קרנו שחשב על תהליכים הפיכים קבע שתהליכים אלו הם היעילים ביותר האפשריים בטבע. כל תהליך שאיננו הפיך יהיה פחות יעיל. לקביעה הפשוטה הזאת יש, כפי שנראה, השלכות מרחיקות לכת, וקרנו ניצל אותה כדי לנתח את הפעולה של מנוע הקיטור. פעולת מנוע הקיטור היא תהליך מורכב שכולל שלבים של חימום וקירור, וקרנו נאלץ לטפל במחזור שלם של פעולות, חלקן בטמפרטורה עולה או יורדת. לעומת זאת, במערכת ההתפלה שלנו אפשר להניח שהטמפרטורה קבועה ואחידה ולכן העניינים פשוטים יותר.

        כעת, כשאנחנו מצוידים בחוק החזק הזה של קרנו הגיע הזמן לעבור להתפלת מים. תמונה -2 מראה כלי הבנוי מצינור מכופף בצורת U אשר בתחתיתו קרום חדיר למחצה שמפריד בין הזרועות שלו. קרום חדיר למחצה הוא קרום שמאפשר מעבר מים דרכו, אבל חוסם מעבר של מלח.

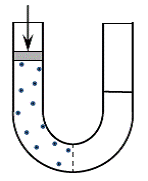
תמונה -2: קרום חדיר למחצה מפריד בין זרועות של צינור מכופף בצורת U המכיל מים. מלח בזרוע השמאלית יוצר בה לחץ אוסמוטי. הלחץ על הבוכנה מעל תמיסת המלח קובע את כוון מעבר המים דרך הקרום.


        מוסיפים מים לכלי וכיוון שהם יכולים לעבור מצד לצד הם יגיעו לאותו גובה בשתי הזרועות שלו, על-פי חוק הכלים השלובים. כעת מוסיפים קצת מלח לזרוע השמאלית. המלח, שאינו יכול לעבור לזרוע האחרת, מתמוסס במים ויוצר בהם לחץ אוסמוטי הגורם למעבר מים מזרוע המים הנקיים אליו, אל זרוע תמיסת המלח. מעבר המים הזה מביא לכך שפני התמיסה יהיו גבוהים מפני המים הנקיים. התהליך הזה של מעבר המים נקרא אוסמוזה. למה נוצר לחץ אוסמוטי? ולמה הוא גורם למעבר המים? בכוונה לא נאמר עכשיו.

        אפשר לעצור את מעבר המים מזרוע לזרוע על-ידי כך שמניחים בוכנה על תמיסת המלח ומפעילים עליה לחץ השווה ללחץ האוסמוטי. כעת המערכת נמצאת במצב סטטי, שום דבר לא זז. אם נגביר את הלחץ על הבוכנה אז היא תרד ומים יתחילו לזרום בכוון הפוך מזרוע התמיסה אל זרוע המים הנקיים. זוהי אוסמוזה הפוכה והתהליך הוא תהליך התפלה כי העברנו מים מתמיסת מלח למים נקיים. אם נפחית בחזרה את הלחץ על הבוכנה לערכו הקודם, אז כוון הזרימה יתחלף שוב, מים יעברו שוב אל התמיסה והבוכנה תעלה ותחזור למקומה הקודם. מהו תהליך זה? נכון, תהליך הפיך. ומה החוק של קרנו אומר לנו עליו? היעיל ביותר האפשרי.

        כאשר הבוכנה דוחפת כמות V של מים דרך הקרום אז העבודה שהיא מבצעת שווה למכפלת הלחץ האוסמוטי בכמות זאת. כך שאנו יודעים כמה אנרגיה יש להשקיע כדי להתפיל כמות מבוקשת של מים. אנרגיה זאת היא האנרגיה המינימלית שיש להשקיע בהתפלה כי התהליך הפיך. בכל תהליך אחר, שאינו הפיך, נצטרך להשקיע יותר אנרגיה.

        האנרגיה המושקעת בדחיפת הבוכנה כלפי מטה שווה בדיוק לאנרגיה המוחזרת מהבוכנה כאשר היא עולה וחוזרת למקומה המקורי. תיאור זה נראה יותר מדי טוב בשביל שיהיה אמיתי. ואמנם בכל אחד מהשלבים יש הפסדים שאי אפשר להימנע מהם לחלוטין. למשל, מעבר המים דרך הקרום כרוך תמיד בהפסד אנרגיה ולא חשוב באיזה כוון המים זורמים. דחיפת הבוכנה כלפי מטה דורשת יותר אנרגיה מאשר בגבול ההפיך, וכאשר היא נדחפת בחזרה למעלה מרוויחים פחות אנרגיה מאשר בגבול ההפיך. אנרגיה הולכת לאיבוד בשני הכיוונים. אפשר רק לנסות להקטין את ההפסד ככל האפשר על-ידי הקטנת קצב מעבר המים. תהליך הפיך הוא, אם כן, הפשטה או גבול של תהליך טבעי שמכיל תמיד הפסד בלתי הפיך כלשהו.

        משיקולים אלו גם ברור שלא ניתן להתפיל מים ללא השקעת אנרגיה כלל. נניח שבדרך פלאית כלשהי הצלחנו להתפיל מים מתמיסה ללא השקעת אנרגיה. ניקח מים אלו ונפיק אנרגיה בכלי שלנו מהחזרת המים לתמיסה בתהליך האוסמוזה, וחוזר חלילה. והרי קבלנו מכונת פרפטום-מובילה שמפיקה אנרגיה יש מאין, שכמובן לא תתכן.

        בסיכום ביניים, יש כאן תהליך של אוסמוזה ואוסמוזה הפוכה שאיננו יודעים עליו כלום, ואף על פי כן, בעזרת החוק של קרנו, אנחנו יודעים עליו המון.

        עד לרעיונות של קרנו השקפת העולם הגשמי הייתה מבוססת על המכניקה של חוקי ניוטון. חוקי ניוטון הם חוקים דטרמיניסטיים. אם ידוע המצב של מערכת, ובכך מתכוונים שידוע המקום של כל החלקיקים במערכת וגם המהירויות שלהם, אז החוקים קובעים בדיוק את המקום שהחלקיקים יהיו בו וגם את המהירות שלהם בכל זמן בעתיד עד סוף כל הדורות. כמו כן, גם את המקום והמהירות שהיו בו בכל זמן בעבר מתחילת כל הדורות. למעשה, יודעים, לא יודעים, לא כל כך חשוב. החוקים פועלים על החלקיקים ממילא. תמונת העולם המקובעת הזאת, שעומדת בסתירה לניסיון היום יום של כל אחד מאתנו, הייתה חידה גדולה במשך תקופה ארוכה.

        במסגרת תמונת העולם המכנית אנשים שאפו להכיר וללמוד את פרטי הפרטים של מערכות כדי שניתן יהיה להפעיל עליהן את חוקי ניוטון ובכך להבין אותן, וכל המרבה בפרטים הרי זה משובח. לעומת זאת, בדוגמה הצנועה שלנו השימוש בחוק של קרנו הביא להבנה של דברים חכמים וחשובים במערכת שכמעט לא מכירים ולא מבינים אותה. במקרים רבים, הידע המפורט, שנדרש בתמונת העולם המכני, בכלל מיותר. בכך החוק של קרנו מרחיב ביותר את המושג מה זה בכלל מדע. אם קודם רק מתימטיקה, פיזיקה, אסטרונומיה, ואולי גם קצת כימיה נחשבו למדעים, החוק של קרנו פתח שער רחב שעברו בו מדעי החיים, כלכלה וכל מדעי החברה, וגם מדעי הרוח. כולם טובים ויפים וכולם באופן טבעי יכולים להגיד דברי טעם על מערכות שמוכרות ומובנות באופן חלקי ביותר.

        לקביעה התמימה כביכול של קרנו שתהליך בלתי הפיך יהיה תמיד פחות יעיל מתהליך הפיך, יש משמעות חשובה אף יותר. נניח שיש תהליך בלתי הפיך כלשהו ואנחנו מצלמים אותו במצלמת וידאו. ברגע מסוים אנחנו עוצרים ומריצים את הסרט בכוון הפוך, דבר שרואים לא פעם בטלוויזיה או בקולנוע. האם הסרט שרץ הפוך, שאנחנו צופים בו, אפשרי בטבע? לפי חוקי ניוטון כן. כל שעלינו לעשות הוא לעצור את המערכת, להפוך את כוון התנועה של כל החלקיקים לאחור במאה ושמונים מעלות, ואז כל חלקיק יחזור למקומו הקודם והמערכת תחזור למצבה בהתחלת הצילום ממש כמו שרואים בסרט. מה אומר החוק של קרנו על כך? ממש אי אפשר. למה? כי אם התהליך המקורי שצלמנו הוא בלתי הפיך ולכן יעילותו קטנה מיעילות תהליך הפיך, אז התהליך שאנחנו רואים בהרצה לאחור של הסרט, שמחזיר כל חלקיק למקומו הקודם ואת המערכת למצבה בהתחלת הצילום, חייב להיות יעיל מיעילות תהליך הפיך, וזה בלתי אפשרי בטבע לפי החוק של קרנו. מי צודק? ניוטון או קרנו? המציאות מלמדת שצודק קרנו. חוקי ניוטון אינם מסוגלים להבחין בין עבר לעתיד. לעומתם, התכונה הזאת של החוק של קרנו, שאי אפשר להחזיר תהליכים בטבע לאחור, פירושה שיש הבדל בין עבר לעתיד. בחוק של קרנו יש משהו חדש שלא קיים בחוקי ניוטון, ולקח הרבה זמן עד שהדבר הזה הובן.

        מתוך העבודה החלוצית של קרנו, יש אומרים "הארה", צמח מדע התרמודינמיקה. היכולת לטפל במערכות שלא יודעים עליהן הרבה הביא להכנסת מושגי הסתברות לתוך התיאוריה, ומתוכם צמח מדע המכניקה הסטטיסטית. פיתוח תורת הקוונטים, בחלק הראשון של המאה העשרים, הביא לכך ש"לא יודעים" התחלף ב"לא יכולים לדעת" ובכך נעלם במידה רבה הקונפליקט עם התמונה הדטרמיניסטית של חוקי ניוטון. התרמודינמיקה והמכניקה הסטטיסטית חדרו לתוך הבסיס של כל ענפי המדע האחרים ואי אפשר יותר בלעדיהן. נזכיר למשל את "החורים השחורים", אותם גופים מוזרים ביקום שבולעים את כל מה שמגיע לקרבתם ולא נודע כי בא אל קרבם. שיקולי תרמודינמיקה מהשנים האחרונות הביאו להבנה שגם גופים אלה מתנדפים לאט לאט ומאבדים את החומר שלהם עד שהם נעלמים.

        אחרי שיטוט בגבהים כאלה הגיע הזמן לנחות בחזרה על קרקע מוצקה ולחזור להתפלת מים. אולי זכורה לנו מימי בית הספר הקילו-קלוריה, יחידת האנרגיה השווה לכמות החום הדרושה לחימום ליטר מים במעלה אחת צלזיוס. כדי לחמם ליטר מים מטמפרטורת סביבה של עשרים מעלות, עד טמפרטורת רתיחה של מאה מעלות, דרושות לכן שמונים קילו-קלוריות. אם רוצים גם להרתיח את המים ולהפוך אותם מנוזל לאדים אז דרושות עוד חמש מאות וארבעים קילו-קלוריות. כמה קילו-קלוריות דרושות כדי להתפיל ליטר מי-ים? האנרגיה המינימלית, לפי קרנו, היא קצת יותר מחצי קילו-קלוריה. במתקני ההתפלה יש הפסדים בלתי נמנעים והאנרגיה הדרושה בפועל היא בין שתים לשלוש קילו-קלוריות. גם כך, האנרגיה שמשקיעים בחימום מים לכוס קפה, עולה לעין ערוך על האנרגיה הדרושה כדי להתפיל את אותם מים.

        תהליך ההתפלה דורש אנרגיה ללא ספק, אבל הוא איננו עתיר אנרגיה, וכיוון שיש מחסור גדול במים במקומות רבים בעולם, שרק ילך ויחמיר, אז אין ברירה אלא להשתמש בו. היום לא היה כדאי להקים את המוביל הארצי. מפעל התפלה אחד גדול יכול לספק את כל כמות המים בהשקעה יותר נמוכה, במחיר יותר זול, והרבה הרבה פחות נזק לסביבה. תהליך חימום מים עתיר אנרגיה הרבה יותר. בשנות השישים של המאה הקודמת התקבל במדינת ישראל חוק המחייב התקנת דוד שמש בכל הדירות החדשות הנבנות. במשך השנים חוק זה הביא לחיסכון גדול באנרגיה ובדלק. מעניין אם מישהו חישב כמה.

        יש מקומות לא רבים בעולם שבהם עודף גדול של מים מתוקים, סקנדינביה או סיביר למשל. במקומות אלה ניתן להפיק אנרגיה בתהליך האוסמוזה מתוך המליחות של מי הים. מקרה מיוחד הוא ים המלח שלנו שמלוח בערך פי עשרה ממי ים רגילים. בעשרות השנים האחרונות מי הירדן נשאבו מים כנרת לצרכי שתיה והשקייה. אם יתנו למי הנהר לזרום שוב אל ים המלח, כפי שהיה בעבר, אז באותה שיטה אפשר יהיה להפיק אנרגיה בשפך הנהר אל הים. בגלל המליחות הגבוהה כמות האנרגיה הניתנת להפקה גבוהה הרבה יותר ובאותה הזדמנות גם מצילים את ים המלח.

        נשאר לנו חוב אחד. מהי בעצם אוסמוזה?

        ההסבר לתופעת האוסמוזה ניתן על-ידי וונט-הוף, כימאי הולנדי, והסבר זה זיכה אותו בפרס נובל הראשון לכימיה בשנת 1901. וונט-הוף עשה אנלוגיה בין התנהגות של חלקיקים בתמיסה לבין התנהגות של מולקולות גז במיכל וקבע שנוסחת הלחץ האוסמוטי בתמיסה זהה לנוסחת הלחץ של גז אידאלי במיכל. מאנלוגיה זאת נובע שהלחץ האוסמוטי אינו תלוי בסוג החלקיקים המומסים, אלא רק פרופורציוני לריכוזם.

        כותב וונט-הוף: "המנגנון שבו, לפי הבנתנו הנוכחית, הלחץ האלסטי של גזים נוצר הוא בהכרח אותו שמביא ללחץ האוסמוטי בתמיסות. הוא תלוי במקרה הראשון, במכות של מולקולות הגז מול דופן הכלי; במקרה השני, במכות של מולקולות החומר המומס בקרום החדיר למחצה, כיוון שהמולקולות של הממיס, שנמצאות בשני הצדדים של הקרום שדרכו הן עוברות, אינן נכנסות לחשבון".

        וונט-הוף היה גם הראשון שהציע מבנה מרחבי תלת-ממדי למולקולה כימית ובכך פתח אופקים רחבים חדשים למקצוע הכימיה וכל מה שבא בעקבותיו. בפרספקטיבה היסטורית עבודה זאת אולי ראויה לא פחות לפרס נובל. וונט-הוף חשב על המבנה התלת-ממדי עוד בתקופה שהיה תלמיד לתואר דוקטור, אבל מישהו יעץ לו לא לפרסם זאת, אלא להגיש עבודה יותר סטנדרטית לקבלת התואר ולפרסם את הרעיון שלו רק אחרי קבלת התעודה. כך באמת עשה.

        למזלו של וונט-הוף נתוני הניסויים על הלחץ האוסמוטי לא היו מספיק ברורים, וכך היה יכול להעביר את התיאוריה שלו. במהרה התברר שנוסחת הלחץ האוסמוטי עובדת במולקולות כמו סוכר, אבל כבר במולקולה פשוטה של מלח שולחן הלחץ האוסמוטי הוא בערך כפול מהלחץ המחושב בנוסחה.

        תוצאה זאת הביאה את ארניוס, כימאי שבדי, להציע כי מולקולה של מלח שולחן מתפרקת ליונים של נתרן וכלור כאשר היא מתמוססת במים. כיוון שכל מולקולה של מלח בנויה משני יונים אלו, אז ריכוזם הכולל בתמיסה יהיה כפול מריכוז המולקולות, ולכן גם הלחץ האוסמוטי יהיה כפול. ארניוס לא קיבל עצה דומה לזאת שקיבל וונט-הוף והגיש את התיאוריה שלו כעבודה לתואר דוקטור. הפרופסורים הבוחנים שלו לא האמינו לו אבל פחדו לפסול אותה. לכן העבירו את העבודה בציון מספיק בקושי, משהו כמו עולה כיתה אך לא בבית ספרנו. ארניוס הפך להיות מדען ידוע עם השנים, תרם עוד תרומות מדעיות חשובות וקיבל גם הוא את פרס נובל בשנת 1903.

        האנלוגיה של וונט-הוף בין הלחץ האוסמוטי ללחץ גז לא התקבלה עם השנים, קמו לה מתנגדים רבים, והיא אינה מקובלת גם היום. היו גם כאלה שטענו, ויש כאלה שטוענים, שהזהות בין הלחץ האוסמוטי ללחץ הגז היא צרוף מקרים בלבד. אין הרבה תועלת בוויכוח בעניין הזה, ומה שאפשר לעשות הוא לצטט את גדולי המדע.

        אדם צעיר ועדיין לא ידוע, אלברט איינשטיין, שהיה בוחן פטנטים מדרגה שלישית במשרד הפטנטים של ברן, כתב בשנת 1905 חמש עבודות מדעיות ששינו את פני העולם, ובעקבות זאת השנה נקראת שנת הפלאות. העבודה השנייה עוסקת בתנועת בראון. בראון היה בוטנאי שהסתכל במיקרוסקופ בחלקיקים זעירים שמרחפים בטיפת מים. החלקיקים לא היו במנוחה אלא רטטו ללא הרף וזזו ממקום למקום בדרך אקראית. בהתחלה קשרו את התופעה לגופים חיים אבל אחר-כך התברר שהיא קיימת גם בחלקיקים דוממים. איינשטיין הסביר את התופעה בכך שמולקולות הנוזל, המקיפות את החלקיק, מכות בו ללא הרף מכל הכיוונים ובכך גורמות לרטיטה שלו.

        למה ההסבר הזה חשוב? כל אחד יודע שהחומרים המרכיבים את העולם בנויים מאטומים שנחשבו פעם לחלקיקי יסוד שאינם ניתנים לחלוקה. היום יודעים שאטום בנוי מגרעין שמכיל פרוטונים ונויטרונים שאותו סובבים אלקטרונים, וגם אלו בנויים מחלקיקים יסודיים יותר. במאה התשע עשרה הדבר לא היה מובן מאליו והיו רבים שחשבו שאטומים לא קיימים באמת, אלא, הם רק נוחות מתמטית שמסייעת בחישובים. אחרי פרסום העבודה של איינשטיין הרעיון שאטומים באמת קיימים הפך להיות נחלת הכלל.

        בפתח העבודה שלו איינשטיין כותב (המקור בגרמנית והתרגום מאנגלית): "אנו חייבים להניח שהחלקיקים המרחפים מבצעים תנועה לא מסודרת - אפילו אם היא מאוד איטית - בנוזל, בגלל התנועה המולקולרית של הנוזל ; אם נמנע מהן לעזוב את הנפח *V בגלל המחיצה, הם יפעילו לחץ על המחיצה בדיוק כמו מולקולות בתמיסה." (המחיצה היא הקרום החדיר למחצה).

        אנריקו פרמי, אחד התורמים החשובים לפיתוח תורת הקוונטים ולפיזיקה גרעינית, וגם הראשון שבנה כור גרעיני, כתב ספר בשם "תרמודינמיקה" שזכה לשבחים רבים על עומק המחשבה ובהירות ההצגה, ונראה שמעטים קוראים אותו . הספר תורגם לעברית בשנות השישים של המאה הקודמת, והנה קטע קצר מתוך הדיון באוסמוזה: "..., יוּגדל הלחץ על אוֹתוֹ דוֹפן של הקרוּם הפּוֹנה לעבר התמיסה, וגידוּל זה סיבּתו בּמוֹלקוּלוֹת החוֹמרים המוּמסים, המכּוֹת בּקרוּם משוּם שאינן יכוֹלוֹת לעבוֹר דרכּוֹ." - אנריקו פרמי, "תרמודינמיקה", תירגם מאנגלית יונתן ברוידא, ערך פרופ' משה ימר, הוצאת יחדיו, תל אביב (1963).

        הדברים מדברים בעד עצמם. כותב דפים אלה חושב שהלחץ האוסמוטי חיוני לשמירת האיזון של התנע הלינארי על התמיסה. זה פחות או יותר מה שאיינשטיין ופרמי אומרים.

        למה המים יכולים לחדור את הקרום החדיר למחצה? הכותב חיפש ולא מצא, הוא משער שהקרום מכיל אתרים הידרופיליים, מושכים מים, ומולקולות המים מדלגות מאתר לאתר וכך עוברות את הקרום.

        בסיכום, הרהורים על מהות המדע ועל המדע והעולם יכולים לבוא מהמפץ הגדול ומהחלקיק האלוהי, וגם מענייני שרברבות.

English version

ברשת: דצמבר 2012 .

אוסמוזה התפלה וקרנו
צינור מים מתוקים במקום תעלת הימים
מהם אוסמוזה אוסמוזה הפוכה ולחץ-אוסמוטי
אנרגית התפלה של מי-ים
מספר אבוגדרו משקל אטומי ומשקל מולקולרי
העיוורים והפיל
האיש הראשון שראיתי
דוליטל הרופא ומאורעותיו
נוסע המחלקה הראשונה
יהודים רוקדים
שלוש פעמים
חלוצים סוללים כביש
יום עיון
סיפורים
Facebook

What do the greatest people of science think on osmosis?

"We must assume that the suspended particles perform an irregular movement - even if a very slow one - in the liquid, on account of the molecular movement of the liquid; if they are prevented from leaving the volume V* by the partition, they will exert a pressure on the partition just like molecules in solution." - Albert Einstein [3].

"Then the pressure on the side of the membrane facing the solution will be increased by the impacts against it of the molecules of the dissolved substances," - Enrico Fermi [4].

See:
Why the osmotic pressure of a solution is equal to a gas pressure of the same particle concentration?
More on Osmosis
Energy of Seawater Desalination
Boltzmann Transport Equation
Osmosis and Thermodynamics
van't Hoff's Evidence

References:

1. S. Carnot, "Reflections on the Motive Power of Fire", Dover Publications, Inc., New York (1960, 1988)
2. J.H. van't Hoff, "Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen", Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
   J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
   translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888)
   J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
   in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
   translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42
3. A. Einstein, "On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat", Originally published in Annalen der Physik 17 [1905]: 549-560
   A. Einstein, "Investigations on the Theory of the Brownian Movement", translated by A.D. Cowper, Dover Publications, Inc., New York, pp. 1-18 (1956)
4. E. Fermi, "Thermodynamics", Dover Publications, Inc., New York (1937) pp. 118-123

By the author:

1. "Thermoelectric Effects Peltier Seebeck and Thomson",
   Abstract: https://urila.tripod.com/Thermoelectric_abstract.htm
   Full page: https://urila.tripod.com/Thermoelectric.pdf, February 2014.
2. "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
3. "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
4. "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
5. "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
6. "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
7. "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
8. "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
9. "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
10. "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
11. "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
12. "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
13. "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
14. "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
15. "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
16. "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).

Links:

1. Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
2. Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
3. The Blind Men and the Elephant
4. My Spin on Lunacy
5. Five Weeks in a Balloon
6. The first man I saw.
7. "Faster, Faster!"
8. Perfection can't be rushed
9. The man higher up
10. Brains
11. The First-Class Passenger
12. other