מהם אוסמוזה אוסמוזה הפוכה ולחץ אוסמוטי
New
Blue Marble the Uniform Earth Image
The Sun and the Moon a Riddle in the Sky
חדש
תקציר: אפקטים תרמואלקטריים פלטייה סיבק ותומסון
מהי אוסמוזה?
זוהי התופעה של מעבר מים דרך קרום חדיר למחצה אשר חוסם מעבר מלחים או מומסים אחרים דרכו.
אוסמוזה היא תהליך יסודי בכל המערכות הביולוגיות. משתמשים בה לטיהור מים ולהתפלה, טיפול בחומרי פסולת,
והרבה תהליכים כימיים וביוכימיים במעבדה ובתעשייה.
כאשר שני נפחים של מים (או של ממס אחר) מופרדים על ידי קרום חדיר למחצה,
המים יעברו מהנפח שבו ריכוז המומס נמוך לנפח שבו ריכוז המומס גבוה. ניתן לעצור את מעבר המים,
או אפילו להפוך את כוון הזרימה, על ידי הפעלת לחץ חיצוני על הנפח בעל הריכוז הגבוה.
במקרה כזה התופעה נקראת אוסמוזה הפוכה.
אם יש פרודות מומסות רק בנפח אחד של המערכת, הלחץ עליו, אשר עוצר את מעבר המים, נקרא לחץ אוסמוטי.
התנועה התרמית של פרודה מומסת, בתוך ממס, מרוסנת על ידי פרודות הממס המקיפות אותה.
תנועת הפרודה המומסת נקבעת כולה על ידי התנגשויות תרמיות עם פרודות הממס השכנות המרטיטות אותה.
למרות זאת, המהירות התרמית הממוצעת שלה שווה למהירות שהייתה לה, אילו הייתה חופשית,
במצב צבירה של גז, ללא פרודות ממס שכנות [3 – 1].
כאשר תנועה של פרודת המומס נחסמת על ידי הקרום היא תעביר אליו תקיפה, ולכן, תיצור עליו לחץ [3 - 2].
כיוון שהמהירות שווה למהירות של פרודה חופשית, הלחץ יהיה שווה ללחץ של גז אידאלי בעל אותו
ריכוז של פרודות. לכן, הלחץ האוסמוטי,
π,
נתון על ידי נוסחת [
4]
ונט הוף,
van't Hoff
, הזהה לנוסחת הלחץ של גז אידאלי
:
π = cRT
כאשר c הוא הריכוז המולרי של המומס, (R = 0.082 (liter∙bar) / (deg∙mol הוא קבוע הגזים, ו- T היא הטמפרטורה בסולם הטמפרטורה המוחלטת (Kelvin).
ונט הוף קיבל את פרס נובל הראשון בכימיה, בשנת 1901, על ההסבר לתופעת האוסמוזה.
למשל, למים אשר מכילים 33 גרם בליטר של סודיום כלוריד (מלח בישול, NaCl), ריכוז אופייני למי ים, יש ריכוז יוני של c = 1.128 מולים לליטר. הצבת ערכים אלו בנוסחת ונט-הוף, עבור טמפרטורת סביבה של T = 300 K, תתן לחץ אוסמוטי של:
π = 1.128 ∙ 0.082 ∙ 300 = 27.8 bar
או, 27.8 קילוגרם לסנטימטר מרובע.
הלחץ האוסמוטי אינו תלוי בסוג המומס, או בגודל הפרודה המומסת, אלא רק בריכוזו המולרי, כפי שמראה הנוסחה.
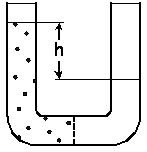
תרשים-1 מראה כלים שלובים המופרדים על-ידי קרום חדיר למחצה. אם ההתקן מכיל רק מים, הגובה שלהם בזרוע אחת יהיה שווה לגובה שלהם בזרוע האחרת. כשמוסיפים פרודות מומסות בזרוע אחת, המים יתחילו לעבור לתוכה, כך שהגובה שלהם יעלה בזרוע זאת וירד בזרוע האחרת. המערכת תתייצב כאשר הלחץ האוסמוטי יאוזן על-ידי הלחץ ההידרוסטטי הנוצר מהבדלי גובה המים h בין הזרועות.
כאשר ρ המשקל הסגולי של המים.
(ρ = gd, כאשר d צפיפות המים ו- g תאוצת הכובד).
חוק שימור האנרגיה וחוק שימור התנע דורשים כי, כל פעם
שחלקיקים מתנגשים עם דופן נעה, הם יהפכו את כוון תנועתם ויגדילו או יקטינו את מהירותם. כך
הם מעבירים גם תקיפה וגם אנרגיה אל הדופן. תהליך ההתנגשויות האלסטיות, עם הדופן הנעה, הוא המנגנון שבו האנרגיה הקינטית
המיקרוסקופית של
החלקיקים הופכת לעבודה מקרוסקופית של הדופן [1].
חק שימור התנע דורש כי
פרודות המומס, היוצרות לחץ אוסמוטי על הקרום החדיר
למחצה, חייבות ליצור, דרך נפח התמיסה, את אותו לחץ אוסמוטי על כל דפנות התמיסה,
כולל הפנים החפשיות שלה.
במובן זה, הלחץ האוסמוטי פועל על פי
חק פסקל.
כאשר מים זורמים דרך הקרום, הלחץ האוסמוטי, הפועל גם על
פני השטח החופשיים של התמיסה, דוחף אותם כלפי מעלה, ובכך הוא אחראי לשאיבת המים מזרוע המים לזרוע התמיסה.
דיון זה במנגנון מעבר המים אינו מופיע בדרך כלל בספרי לימוד שעוסקים
באוסמוזה. השפעת הלחץ האוסמוטי על הפנים
החופשיות של התמיסה הוצע לראשונה על-ידי Hulet ב- 1902 [5], אך זכה לתשומת לב מועטה. נראה
כי מאז היו לו רק מעט תומכים [15 – 6].
אוסמוזה היא תהליך תרמודינמי הפיך. זאת אומרת, מעבר המים, דרך הקרום החדיר למחצה, יכול להפוך כוון בכל רגע ורגע, על-ידי שליטה
נכונה בלחץ החיצוני על התמיסה. בניגוד לכך, ערבוב כפית סוכר והמסתו בכוס תה הוא תהליך בלתי הפיך
של דיפוזיה של סוכר במים. אין דרך להפוך את כוון התהליך, בכל רגע ורגע, ולהחזיר כך את הסוכר המומס בחזרה אל הכפית.
הפיכות היא רעיון עיקרי של
התרמודינמיקה. אוסמוזה היא תהליך הפיך, ולעומת זאת דיפוזיה של סוכר במים איננה תהליך הפיך. דיפוזיה היא תהליך בלתי הפיך.
כדי להפיק מי-שתיה ממי-ים, בשיטת האוסמוזה ההפוכה, יש
להפעיל על המים המלוחים לחץ p גבוה מהלחץ האוסמוטי, כדי
שמים נקיים יעברו את הקרום החדיר למחצה, ויצטברו בצדו האחר. הפקת מי-השתיה דורשת השקעת אנרגיה E שערכה:
E = p∙V / 36
עבור E בקילו-ווט שעה, p ב-בר, ו-V במטרים מעוקבים.
אם הלחץ p נמוך מהלחץ האוסמוטי, אז
המים הנקיים יעברו בחזרה דרך הקרום אל המים
המלוחים. בתהליך זה ניתן להפיק אנרגיה מ"ערבוב" מים נקיים עם מים מלוחים דרך קרום חדיר למחצה.
אי אפשר להפיק מים נקיים ממי-ים, בתהליך כלשהו, בלי השקעת אנרגיה. אילו הדבר היה אפשרי, היה ניתן
להפיק כמות מים נקיים ללא השקעת אנרגיה, אחר-כך ל"ערבב" אותם דרך קרום חדיר למחצה ולהרוויח אנרגיה, וחוזר
חלילה. זהו תהליך "פרפטום-מובילה", שבו מקבלים אנרגיה יש מאין, והוא בלתי אפשרי.
האנרגיה המינימלית הדרושה להפקת מי שתיה מחושבת על ידי הצבת הלחץ האוסמוטי π בנוסחה. האנרגיה המינימלית עבור הלחץ שחושב היא:
E = 27.8 ∙ 1 / 36 = 0.77 (kWatt hour) / (cubic meter) = 0.66 kcal / liter
בהשוואה לכך, קילו-קלוריה אחת דרושה כדי לחמם ליטר מים במעלה אחת צלזיוס, ו- 540 קילו-קלוריות דרושות כדי להרתיח ליטר מים.
מה גדולי המדע של כל הזמנים חושבים על אוסמוזה ?
"אנו חייבים להניח שהחלקיקים המרחפים מבצעים תנועה לא מסודרת - אפילו אם היא מאוד איטית - בנוזל, בגלל
התנועה המולקולרית של הנוזל ; אם נמנע מהן לעזוב את הנפח *V בגלל המחיצה, הם
יפעילו לחץ על המחיצה בדיוק כמו מולקולות בתמיסה." - אלברט אינשטין [2].
"..., יוּגדל הלחץ על אוֹתוֹ דוֹפן של הקרוּם הפּוֹנה לעבר התמיסה, וגידוּל זה סיבּתו
בּמוֹלקוּלוֹת החוֹמרים המוּמסים, המכּוֹת בּקרוּם משוּם שאינן יכוֹלוֹת לעבוֹר דרכּוֹ." - אנריקו פרמי [3], "תרמודינמיקה", תירגם מאנגלית יונתן ברוידא,
ערך פרופ' משה ימר, הוצאת יחדיו, תל אביב (1963).
עברית: אוקטובר 2005
.
אוסמוזה התפלה וקרנו
צינור מים מתוקים במקום תעלת הימים
מהם אוסמוזה אוסמוזה הפוכה ולחץ-אוסמוטי
אנרגית התפלה של מי-ים
מספר אבוגדרו משקל אטומי ומשקל מולקולרי
העיוורים והפיל
האיש הראשון שראיתי
דוליטל הרופא ומאורעותיו
נוסע המחלקה הראשונה
יהודים רוקדים
שלוש פעמים
חלוצים סוללים כביש
יום עיון
סיפורים
Facebook
What do the greatest people of science think on osmosis?
"We must assume that the suspended particles perform an irregular movement - even if a very slow
one - in the liquid, on account of the molecular movement of the liquid; if they are
prevented from leaving the volume V* by the partition, they will exert a pressure
on the partition just like molecules in solution." - Albert Einstein [2].
"Then the pressure on the side of the membrane facing the solution will be increased by the
impacts against it of the molecules of the dissolved substances," - Enrico Fermi [3].
See:
Why the osmotic pressure of a solution is equal to a gas pressure of the same particle concentration?
More on Osmosis
Energy of Seawater Desalination
Osmosis and Thermodynamics
van't Hoff's Evidence
References:
- F.W. Sears and G.L. Salinger, "Thermodynamics, Kinetic Theory and statistical Thermodynamics", 3rd Ed., 16th printing, Addison Wesley, Reading Massachusetts (1986) pp. 250-266
- A. Einstein, "On
the Motion of Small Particles Suspended in Liquids at Rest
Required by the Molecular-Kinetic Theory of Heat",
Originally published in Annalen der Physik 17 [1905]: 549-560
A. Einstein, "Investigations on the Theory of the Brownian Movement", translated by A.D. Cowper, Dover Publications, Inc., New York, pp. 1-18 (1956) - E. Fermi, "Thermodynamics", Dover Publications, Inc., New York (1937) pp. 118-123
- J.H. van't Hoff,
"Die Rolle osmotischen Drucks in der Analogie zwischen Losungen und Gasen",
Zeitschrift fur physikalische Chemie, vol 1, pp. 481-508 (1887)
J.H. van't Hoff, "The Function of Osmotic Pressure in the Analogy between Solutions and Gases",
translated by W. Ramsay, Philosophical Magazine, S. 5. vol 26. No. 159. Aug, pp. 81-105 (1888) J.H. van't Hoff, "The Role of Osmotic Pressure in the Analogy between Solutions and Gases",
in: The Modern Theory of Solution, Memoirs by Pfeffer, van't Hoff, Arrhenius, and Raoult,
translated and edited by Harry C. Jones, Harper & Brothers Publishers, New York and London, pp. 11-42 (1899) - G.A. Hulett, Acta. Phys. Chem. 42, 353 (1902)
- K.F. Herzfeld, Phys. Z. 38, 58 (1937)
- K.J. Mysels and S.C. Copeland, "Introduction to the Science of Chemistry", Ginn and Co., Boston (1952) p. 127
- K.J. Mysels, "Introduction to Colloid Chemistry", Interscience, New york (1959) Ch. VI
- P.F. Scholander, Proc. Natl. Acad. Sci. U.S.A., 55, 1407 (1966)
- P.F. Scholander, Microvasc. Res., 3, 215 (1971)
- H.T. Hammel and P.F. Scholander, "Osmosis and Tensile Solvent", Springer, New York (1976)
- H.T. Hammel, Science, 192, 748 (1976)
- K.J. Mysels, J. Chem. Ed., 55, 21 (1978)
- U. Lachish, J. Chem. Ed., 55, 369 (1978)
- K.J. Mysels, J. Phys. Chem. B, 101, 1893 (1997), and references therein.
On the net: February, revised, October, 1998. References added, October,
1999.
Download as pdf: https://urila.tripod.com/index.pdf
By the author:
- "Thermoelectric Effects Peltier Seebeck and Thomson",
Abstract: https://urila.tripod.com/Thermoelectric_abstract.htm
Full page: https://urila.tripod.com/Thermoelectric.pdf, February 2014. - "Osmosis Desalination and Carnot", https://urila.tripod.com/Osmosis_Carnot.htm, December 2012.
- "Light Scattering", https://urila.tripod.com/scatter.htm, August (2011).
- "The Sun and the Moon a Riddle in the Sky", https://urila.tripod.com/moon.htm, July (2011).
- "Osmosis and thermodynamics", American Journal of Physics, Vol 75 (11), pp. 997-998, November (2007).
- "van't Hoff's Evidence", https://urila.tripod.com/evidence.htm, October (2007).
- "Osmosis and Thermodynamics", https://urila.tripod.com/osmotic.htm, January (2007).
- "Expansion of an ideal gas", https://urila.tripod.com/expand.htm, December (2002).
- "Optimizing the Efficiency of Reverse Osmosis Seawater Desalination", https://urila.tripod.com/Seawater.htm, May (2002).
- "Boltzmann Transport Equation", https://urila.tripod.com/Boltzmann.htm, May (2002).
- "Energy of Seawater Desalination", https://urila.tripod.com/desalination.htm, April (2000).
- "Avogadro's number atomic and molecular weight", https://urila.tripod.com/mole.htm, April (2000).
- "Vapor Pressure, Boiling and Freezing Temperatures of a Solution", https://urila.tripod.com/colligative.htm, December (1998).
- "Osmosis Reverse Osmosis and Osmotic Pressure what they are", https://urila.tripod.com/index.htm, February (1998).
- "Calculation of linear coefficients in irreversible processes by kinetic arguments", American Journal of Physics, Vol 46 (11), pp. 1163-1164, November (1978).
- "Derivation of some basic properties of ideal gases and solutions from processes of elastic collisions", Journal of Chemical Education, Vol 55 (6), pp. 369-371, June (1978).
Links:
- Thermodynamics Research Laboratory, http://www.uic.edu/~mansoori/Thermodynamics.Educational.Sites_html
- Thermodynamik - Warmelehre, http://www.schulphysik.de/thermodyn.html
- The Blind Men and the Elephant
- My Spin on Lunacy
- Five Weeks in a Balloon
- The first man I saw.
- "Faster, Faster!"
- Perfection can't be rushed
- The man higher up
- Brains
- The First-Class Passenger
- other